


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源:不详 题型:单选题
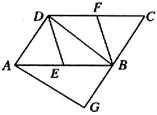
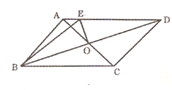
 ABCD中 ,E是BC的中点,且∠AEC=∠DCE,下列结论中正确的有
ABCD中 ,E是BC的中点,且∠AEC=∠DCE,下列结论中正确的有 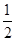 DF 2.S△AFD=2S△EFB
DF 2.S△AFD=2S△EFB| A.1个 | B.2个 | C.3个 | D.4个() |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
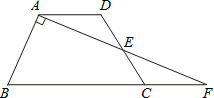
科目:初中数学 来源:不详 题型:单选题

| A.△AED≌△BFA | B.DE﹣BF=EF | C.△BGF∽△DAE | D.DE﹣BG=FG |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ABCD 中, AB
ABCD 中, AB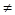 AD ,对角线 AC 与 BD 相交于点 O , OE⊥BD交 AD 于 E ,若△ABE 的周长为 12cm ,则
AD ,对角线 AC 与 BD 相交于点 O , OE⊥BD交 AD 于 E ,若△ABE 的周长为 12cm ,则 ABCD的周长是
ABCD的周长是 | A.24cm | B.40cm | C.48cm | D.无法确定 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.同一边上两个角相等的梯形是等腰梯形; |
| B.一组对边平行,一组对边相等的四边形是平行四边形; |
| C.如果顺次连结一个四边形各边中点得到的是一个正方形,那么原四边形一定是正方形。 |
| D.对角线互相垂直的四边形面积等于对角线乘积的一半。 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com