练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
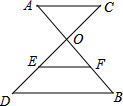
    13．如图，AB、CD相交于点O，OC=4，OD=6，AC∥BD，EF是△ODB的中位线，且EF=4，则AC的长为$\frac{16}{3}$．

    分析 根据三角形中位线定理求出BD，根据相似三角形的性质列出比例式，计算即可．

    解答 解：∵EF是△ODB的中位线，
    ∴BD=2EF=8，
    ∵AC∥BD，
    ∴$\frac{AC}{BD}$=$\frac{OC}{OD}$，即$\frac{AC}{8}$=$\frac{4}{6}$，
    解得，AC=$\frac{16}{3}$，
    故答案为：$\frac{16}{3}$．

    点评 本题考查的是三角形的中位线的性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    3．如图所示，在平面直角坐标系中，抛物线y=ax2+bx+3（a≠0）经过A（-3，0）、B（1，0）两点，与y轴交于点C，其顶点为D，连接AD，点P事线段AD上一个动点（不与A、D重合），过点P作y轴的垂线PE，垂足点为E，连接AE．
    （1）求抛物线的函数解析式，并写出顶点D的坐标；
    （2）如果P点的坐标为（x，y），△PAE的面积为S，求S与x之间的函数关系式，直接写出自变量x的取值范围，并求出S的最大值；
    （3）在（2）的条件下，当S取到最大值时，过点P作x轴的垂线PF，垂足为F，连接EF，把△PEF沿直线EF折叠，点P的对应点为点P′，求出P′的坐标，并判断P′是否在该抛物线上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．某机构对2016年微信用户的职业颁布进行了随机抽样调查（职业说明：A：党政机关、军队，B：事业单位，C：企业，D：自由职业及人体户，E：学生，F：其他），图1和图2是根据调查数据绘制而成的不完整的统计图．请根据图中提供的信息，解答下列问题：

    （1）该机构共抽查微信用户50000人；
    （2）在图1中，补全条形统计图；
    （3）在图2中，“D”用户所对应扇形的圆心角度数为90度；
    （4）2016年微信用户约有7.5亿人，估计“E”用户大约有1.08亿人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

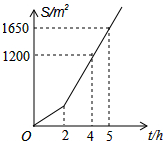    1．明君社区有一块空地需要绿化，某绿化组承担了此项任务，绿化组工作一段时间后，提高了工作效率．该绿化组完成的绿化面积S（单位：m2）与工作时间t（单位：h）之间的函数关系如图所示，则该绿化组提高工作效率前每小时完成的绿化面积是150m2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．计算：（2017-π）0-（-3）-2=$\frac{8}{9}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．在平面直角坐标系中，点P（-1，2）沿x轴向右平移3个单位长度得到的点的坐标为（2，2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．如图，半径为2的半圆形纸片，按如图方式折叠，使对折后半圆弧的中点M与圆心O重合，则图中阴影部分的面积是（　　）
    A．18$\sqrt{3}$-6πB．4$\sqrt{3}$-$\frac{4}{3}$πC．9$\sqrt{3}$-$\frac{9}{2}$πD．2$\sqrt{3}$-$\frac{2}{3}$π

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

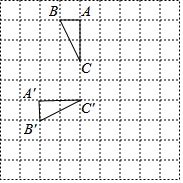    2．如图，在边长为1的小正方形网格中，将△ABC绕某点旋转到△A'B'C'的位置，则点B运动的最短路径长为$\frac{\sqrt{13}}{2}$π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．某农科院要考察某种幼树在一定条件下的移植成活率，下表是这种幼树在移植过程中的一组统计数据：
    移植总数100400750150035007000900014000
    成活数83314606119728105613719411208
    成活的频率0.830.7850.8080.7980.8030.8020.7990.801
    则该幼树移植成活的概率估计值为0.8（结果精确到0.1）．

    查看答案和解析>>

    同步练习册答案