
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6。P是AB边上的一个动点(异于A、B两点),过点P分别作AC、BC边的垂线,垂足为M、N设AP=x。

(1)在△ABC中,AB= ;
(2)当x= 时,矩形PMCN的周长是14;
(3)是否存在x的值,使得△PAM的面积、△PBN的面积与矩形PMCN的面积同时相等?请说出你的判断,并加以说明。
【答案】(1)10;(2)5;(3)不存在
【解析】
试题分析:(1)仔细分析题意利用勾股定理求解即可;
(2)利用MP∥BC和NP∥AC,可得到![]() ,
,![]() ,将AP=x,AB=10,BC=6,AC=8,BP=10-x
,将AP=x,AB=10,BC=6,AC=8,BP=10-x
代入式中就能得到PM和PN关于x的表达式.再由矩形周长=2(PM+PN),求出x的值.
(3)当P为AB的中点时,△PAM的面积与△PBN的面积才相等,再求出矩形PMCN的面积,进行判断.
(1)∵△ABC为直角三角形,且AC=8,BC=6,
![]()
(2))∵PM⊥AC PN⊥BC
∴MP∥BC,AC∥PN(垂直于同一条直线的两条直线平行),
∴![]() ,
,![]()
∵AP=x,AB=10,BC=6,AC=8,BP=10-x,
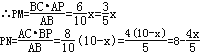
∴矩形PMCN周长=2(PM+PN)=2(![]() x+8-
x+8-![]() x)=14,解得x=5;
x)=14,解得x=5;
(3)∵PM⊥AC,PN⊥BC,
∴∠AMP=∠PNB=∠C=90.
∴AC∥PN,∠A=∠NPB.
∴△AMP∽△PNB∽△ABC.
当P为AB中点时,可得△AMP≌△PNB
此时S△AMP=S△PNB=![]() ×4×3=6
×4×3=6
而S矩形PMCN=PM·MC=3×4=12.
所以不存在x的值,能使△AMP的面积、△PNB的面积与矩形PMCN面积同时相等.


科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
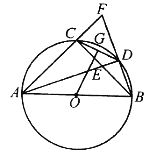
【题目】如图, ![]() 内接于⊙
内接于⊙![]() ,
, ![]() ,
, ![]() 的平分线
的平分线![]() 与⊙
与⊙![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,延长
,延长![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() ,
, ![]() 是
是![]() 的中点,连接
的中点,连接![]() .
.
(1)判断![]() 与
与![]() 的位置关系,写出你的结论并证明;
的位置关系,写出你的结论并证明;
(2)求证: ![]() ;
;
(3)若![]() ,求⊙
,求⊙![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
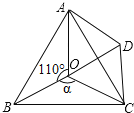
(1)求证:△COD是等边三角形;
(2)当a=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当a为多少度时,△AOD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a﹣b|.
![]()
(1)计算2⊙(﹣3)的值;
(2)当a,b在数轴上的位置如图所示时,化简a⊙b;
(3)已知(a⊙a)⊙a=8+a,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
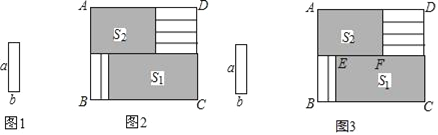
【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,求a,b满足的关系式.
(1)为解决上述问题,如图3,小明设EF=x,则可以表示出S1=_________,S2=_________;
(2)求a,b满足的关系式,写出推导过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和同桌小聪在课后复习时,对练习册“目标与评定”中的一道思考题,进行了认真地探索.
(思考题)如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
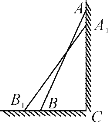
(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则A1B1=2.5,在Rt△A1B1C中,由B1C2+A1C2=A1B12,
得方程___________________,解方程,得x1=____,x2=______________,∴点B将向外移动____米.
(2)解完“思考题”后,小聪提出了如下两个问题:
(问题一)在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(问题二)在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为直线AB上的一点,射线OA表示正北方向,∠COE=90°,射线OF平分∠AOE.
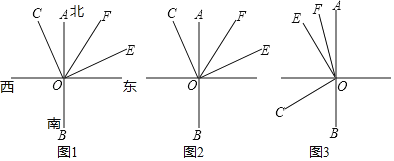
(1)如图1,若∠AOE=70°,则∠COF的度数是 ;
(2)若将∠COE绕点O旋转至图2的位置,试判断∠COF和∠BOE之间的数量关系,并证明你的证明;
(3)若将∠COE绕点O旋转至图3的位置,直接写出2∠COF+∠BOE的度数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com