
ЗжЮі ЃЈ1ЃЉЗжБ№ЧѓГіУПвЛИіВЛЕШЪНЕФНтМЏЃЌИљОнПкОїЃКЭЌДѓШЁДѓЁЂЭЌаЁШЁаЁЁЂДѓаЁаЁДѓжаМфевЁЂДѓДѓаЁаЁЮоНтСЫШЗЖЈВЛЕШЪНзщЕФНтМЏЃЛ
ЃЈ2ЃЉЗжБ№ЧѓГіУПвЛИіВЛЕШЪНЕФНтМЏЃЌИљОнПкОїЃКЭЌДѓШЁДѓЁЂЭЌаЁШЁаЁЁЂДѓаЁаЁДѓжаМфевЁЂДѓДѓаЁаЁЮоНтСЫШЗЖЈВЛЕШЪНзщЕФНтМЏЃЎ
НтД№ НтЃКЃЈ1ЃЉНтВЛЕШЪН$\frac{1}{2}$x-1Ём7-$\frac{3}{2}$xЃЌЕУЃКxЁм4ЃЌ
НтВЛЕШЪН5x-2ЃО3ЃЈx+1ЃЉЃЌЕУЃКxЃО$\frac{5}{2}$ЃЌ
ЁрВЛЕШЪНзщЕФНтМЏЮЊ$\frac{5}{2}$ЃМxЁм4ЃЌ
БэЪОдкЪ§жсЩЯШчЯТЃК
ЃЈ2ЃЉНтВЛЕШЪН2x+5Ём3ЃЈx+2ЃЉЃЌЕУЃКxЁн-1ЃЌ
НтВЛЕШЪН2x-$\frac{1+3x}{2}$ЃМ1ЃЌЕУЃКxЃМ3ЃЌ
ЁрВЛЕШЪНзщЕФНтМЏЮЊ-1ЁмxЃМ3ЃЌ
БэЪОдкЪ§жсЩЯШчЯТЃК
ЕуЦР БОЬтПМВщЕФЪЧНтвЛдЊвЛДЮВЛЕШЪНзщЃЌе§ШЗЧѓГіУПвЛИіВЛЕШЪННтМЏЪЧЛљДЁЃЌЪьжЊЁАЭЌДѓШЁДѓЃЛЭЌаЁШЁаЁЃЛДѓаЁаЁДѓжаМфевЃЛДѓДѓаЁаЁевВЛЕНЁБЕФддђЪЧНтД№ДЫЬтЕФЙиМќЃЎ


 ЗЂЩЂЫМЮЌаТПЮЬУЯЕСаД№АИ
ЗЂЩЂЫМЮЌаТПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 дквЛДЮЛЇЭтЭиеЙбЕСЗжаЃЌаЁУїХЪЕНвЛИіИпЮЊ10УзЕФИпЕиAДІЃЈШчЭМЃЉПДЕНаќбТЖЅВПOЕФбіНЧЮЊ30ЁуЃЌРћгУЙвдкаќбТЖЅВПЕФЩўЫїЃЌЛЎЙ§90ЁуЕНДяИпЮЊ3УзЕФЦНЬЈBДІЃЌЧѓЩўЫїOAЕФГЄЖШКЭаЁУїдкЕДЩўЫїЕФЙ§ГЬжаРыЕиУцЕФзюЕЭЕуЕФИпЖШMNЃЎЃЈаЁУїЕФЩэИпКіТдВЛМЦЃЌНсЙћОЋШЗЕН0.01УзЃЌВЮПМЪ§ОнЃК$\sqrt{2}$Ёж1.414ЃЌ$\sqrt{3}$Ёж1.732ЃЉ
дквЛДЮЛЇЭтЭиеЙбЕСЗжаЃЌаЁУїХЪЕНвЛИіИпЮЊ10УзЕФИпЕиAДІЃЈШчЭМЃЉПДЕНаќбТЖЅВПOЕФбіНЧЮЊ30ЁуЃЌРћгУЙвдкаќбТЖЅВПЕФЩўЫїЃЌЛЎЙ§90ЁуЕНДяИпЮЊ3УзЕФЦНЬЈBДІЃЌЧѓЩўЫїOAЕФГЄЖШКЭаЁУїдкЕДЩўЫїЕФЙ§ГЬжаРыЕиУцЕФзюЕЭЕуЕФИпЖШMNЃЎЃЈаЁУїЕФЩэИпКіТдВЛМЦЃЌНсЙћОЋШЗЕН0.01УзЃЌВЮПМЪ§ОнЃК$\sqrt{2}$Ёж1.414ЃЌ$\sqrt{3}$Ёж1.732ЃЉВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
 ШчЭМЃЌдк3ЁС3ЕФЗНИёФкЃЌЬюаДСЫвЛаЉЕЅЯюЪНЃЌвбжЊЭМжаИїааЁЂИїСаМАЖдНЧЯпЩЯШ§ИіЕЅЯюЪНжЎКЭЖМЯрЕШЃЌдђxЕФжЕгІЮЊ-1ЃЎ
ШчЭМЃЌдк3ЁС3ЕФЗНИёФкЃЌЬюаДСЫвЛаЉЕЅЯюЪНЃЌвбжЊЭМжаИїааЁЂИїСаМАЖдНЧЯпЩЯШ§ИіЕЅЯюЪНжЎКЭЖМЯрЕШЃЌдђxЕФжЕгІЮЊ-1ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
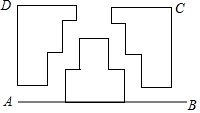 ШчЭМЃЌЫФБпаЮABCDЪЧвЛПщГЄЗНаЮГЁЕиЃЌAB=42УзЃЌAD=25УзЃЌДгAЃЌBСНДІШыПкЕФаЁТЗПэЖМЮЊ1УзЃЌСНаЁТЗЛиКЯДІТЗПэЮЊ2УзЃЌЦфгрВПЗжжжжВВнЦКЃЌдђВнЦКУцЛ§ЮЊ960ЦНЗНУзЃЎ
ШчЭМЃЌЫФБпаЮABCDЪЧвЛПщГЄЗНаЮГЁЕиЃЌAB=42УзЃЌAD=25УзЃЌДгAЃЌBСНДІШыПкЕФаЁТЗПэЖМЮЊ1УзЃЌСНаЁТЗЛиКЯДІТЗПэЮЊ2УзЃЌЦфгрВПЗжжжжВВнЦКЃЌдђВнЦКУцЛ§ЮЊ960ЦНЗНУзЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
 ШчЭМЃЌЕШБпЁїABCжаЃЌЕуEЁЂFЗжБ№ЪЧABЁЂACЕФжаЕуЃЌдђЁЯEFBЕФЖШЪ§ЮЊЃЈЁЁЁЁЃЉ
ШчЭМЃЌЕШБпЁїABCжаЃЌЕуEЁЂFЗжБ№ЪЧABЁЂACЕФжаЕуЃЌдђЁЯEFBЕФЖШЪ§ЮЊЃЈЁЁЁЁЃЉ| AЃЎ | 25Ёу | BЃЎ | 30Ёу | CЃЎ | 35Ёу | DЃЎ | 40Ёу |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ЃЈ0ЃЌ10ЃЉ | BЃЎ | ЃЈ5ЃЌ0ЃЉ | CЃЎ | ЃЈ0ЃЌ-5ЃЉ | DЃЎ | ЃЈ0ЃЌ4ЃЉ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com