
【题目】如图,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() ,双曲线
,双曲线![]() ,的图象经过
,的图象经过![]() 上的点
上的点![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,若若
,若若![]() 是
是![]() 的中点﹒
的中点﹒
(1)求![]() 点的坐标;
点的坐标;
(2)点![]() 是
是![]() 边上一点,若
边上一点,若![]() 和
和![]() 相似,求
相似,求![]() 的解析式;
的解析式;
(3)若点![]() 也在此反比例函数的图象上(其中
也在此反比例函数的图象上(其中![]() ),过
),过![]() 点作
点作![]() 轴的垂线,交
轴的垂线,交![]() 轴于点
轴于点![]() ,若线段
,若线段![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 的面积是
的面积是![]() ,设
,设![]() 点的纵坐标为
点的纵坐标为![]() ,求
,求![]() 的值.
的值.
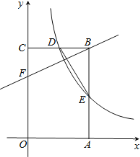
【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() 的解析式为:
的解析式为:![]() ,或
,或![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求出点E的坐标,求出双曲线的解析式,再求出CD=1,即可得出点D的坐标;
(2)分两种情况:①△FBC和△DEB相似,当BD和BC是对应边时,![]() ,求出CF,得出F的坐标,用待定系数法即可求出直线BF的解析式;
,求出CF,得出F的坐标,用待定系数法即可求出直线BF的解析式;
②当BD与CF是对应边时,![]() ,求出CF、OF,得出F的坐标,用待定系数法即可求出直线BF的解析式;
,求出CF、OF,得出F的坐标,用待定系数法即可求出直线BF的解析式;
(3)由题意得出m(3m+6 )=3,即m2+2m﹣1=0,由三角形的面积得出mn=1,代入得出n2﹣2n=1,即可得出所求式子的值.
(1)∵四边形ABCD是矩形,∴OA=BC,AB=OC.
∵B(2,3),E为AB的中点,∴AB=OC=3,OA=BC=2,AE=BE![]() AB
AB![]() ,∴E(2,
,∴E(2,![]() ),∴k=2
),∴k=2![]() 3,∴双曲线解析式为:y
3,∴双曲线解析式为:y![]() ;
;
∵点D在双曲线y![]() (x>0)上,∴OCCD=3,∴CD=1,∴点D的坐标为:(1,3);
(x>0)上,∴OCCD=3,∴CD=1,∴点D的坐标为:(1,3);
(2)∵BC=2,CD=1,∴BD=1,分两种情况:
①△FBC和△DEB相似,当BD和BC是对应边时,![]() ,即
,即![]() ,∴CF=3,∴F(0,0),即F与O重合,设直线BF的解析式为:y=kx,把点B(2,3)代入得:k
,∴CF=3,∴F(0,0),即F与O重合,设直线BF的解析式为:y=kx,把点B(2,3)代入得:k![]() ,∴直线/span>BF的解析式为:y
,∴直线/span>BF的解析式为:y![]() x;
x;
②△FBC和△DEB相似,当BD与CF是对应边时,![]() ,即
,即![]() ,∴CF
,∴CF![]() ,∴OF=3
,∴OF=3![]() ,∴F(0,
,∴F(0,![]() ),设直线BF的解析式为:y=ax+c,把B(2,3),F(0,
),设直线BF的解析式为:y=ax+c,把B(2,3),F(0,![]() )代入得:
)代入得: ,解得:a
,解得:a![]() ,c
,c![]() ,∴直线BF的解析式为:y
,∴直线BF的解析式为:y![]() ;
;
综上所述:若△FBC和△DEB相似,BF的解析式为:y![]() x或y
x或y![]() ;
;
(3)∵点P(m,3m+6)在反比例函数y![]() 的图象上,∴m(3m+6 )=3,整理得:m2+2m﹣1=0.
的图象上,∴m(3m+6 )=3,整理得:m2+2m﹣1=0.
∵PQ⊥x轴,∴Q点的坐标为:(m,n).
∵△OQM的面积为![]() ,∴
,∴![]() OMQM
OMQM![]() ,∴OMQM=1.
,∴OMQM=1.
∵m>0,∴mn=1,∴m![]() ,代入m2+2m﹣1=0得:
,代入m2+2m﹣1=0得:![]() 1=0,即n2﹣2n﹣1=0,∴n2﹣2n=1,∴n2﹣2n+9=10.
1=0,即n2﹣2n﹣1=0,∴n2﹣2n=1,∴n2﹣2n+9=10.


科目:初中数学 来源: 题型:
【题目】如图1,已知正方形![]() 的边长为1,点
的边长为1,点![]() 在边
在边![]() 上,若
上,若![]() ,且
,且![]() 交正方形外角的平分线
交正方形外角的平分线![]() 于点
于点![]() .
.
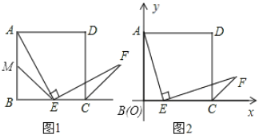
(1)如图1,若点![]() 是边
是边![]() 的中点,
的中点,![]() 是边
是边![]() 的中点,连接
的中点,连接![]() ,求证:
,求证:![]() .
.
(2)如图2,若点![]() 在线段
在线段![]() 上滑动(不与点
上滑动(不与点![]() ,
,![]() 重合).
重合).
①在点![]() 滑动过程中,
滑动过程中,![]() 是否一定成立?请说明理由;
是否一定成立?请说明理由;
②在如图所示的直角坐标系中,当点![]() 滑动到某处时,点
滑动到某处时,点![]() 恰好落在直线
恰好落在直线![]() 上,求此时点
上,求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,AB在x轴上,以AB为直径的半圆⊙O‘与y轴正半轴交于点C,连接BC,AC.CD是半圆⊙O’的切线,AD⊥CD于点D

(1)求证:∠CAD =∠CAB(3分)
(2)已知抛物线![]() 过A、B、C三点,AB=10,tan∠CAD=
过A、B、C三点,AB=10,tan∠CAD=![]() .
.
① 求抛物线的解析式(3分)
② 判断抛物线的顶点E是否在直线CD上,并说明理由(3分);
③ 在抛物线上是否存在一点P,使四边形PBCA是直角梯形.若存在,直接写出点P的坐标(不写求解过程);若不存在,请说明理由(3分).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为点D,点E,BE、CD相交于点O.∠1=∠2,则图中全等三角形共有( )
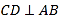
A. 4对B. 3对C. 2对D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
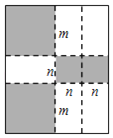
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小矩形,且m>n.(以上长度单位:cm)
(1)观察图形,可以发现代数式2m2+5mn+2n2可以因式分解为 ;
(2)若每块小矩形的面积为10cm2,两个大正方形和两个小正方形的面积和为58cm2,试求m+n的值
(3)②图中所有裁剪线(虚线部分)长之和为 cm.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装店在服装销售中发现:进货价每件60元,销售价每件100元的某童装每天可售出20件![]() 为了迎接“六一儿童节”,童装店决定采取适当的促销措施,扩大销售量,增加盈利
为了迎接“六一儿童节”,童装店决定采取适当的促销措施,扩大销售量,增加盈利![]() 经调查发现:如果每件童装降价1元,那么每天就可多售出2件.
经调查发现:如果每件童装降价1元,那么每天就可多售出2件.
![]() 如果童装店想每天销售这种童装盈利1050元,同时又要使顾客得到更多的实惠,那么每件童装应降价多少元?
如果童装店想每天销售这种童装盈利1050元,同时又要使顾客得到更多的实惠,那么每件童装应降价多少元?
![]() 每件童装降价多少元时,童装店每天可获得最大利润?最大利润是多少元?
每件童装降价多少元时,童装店每天可获得最大利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标上数字-1、1、2.随机摸出一个小球(不放回),其数字记为p,再随机摸出另一个小球,其数字记为q,则p,q使关于x的方程x2+px+q=0有实数根的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com