
【题目】如图,已知抛物线y=ax2+bx+c经过点A(-1,0)、B(3,0)、C(0,3)三点.
(1)求抛物线相应的函数表达式;
(2)点M是线段BC上的点(不与B、C重合),过M作MN∥y轴交抛物线于N,连接NB.若点M的横坐标为t,是否存在t,使MN的长最大?若存在,求出sin∠MBN的值;若不存在,请说明理由;
(3)若对一切x≥0均有ax2+bx+c≤mx-m+13成立,求实数m的取值范围.

【答案】(1)y=-x2+2x+3;(2)存在,sin∠MBN=![]() ;(3)-6≤m≤10.
;(3)-6≤m≤10.
【解析】
(1)用待定系数法即可求出抛物线的解析式;
(2)先求出直线BC的解析式,设M(t,-t+3),N(t,-t2+2t+3),得出MN是t的二次函数,即可求出MN的最大值;延长NM交OB于E,证出△BME为等腰直角三角形,求出BE、BM、BN,过点M作△BNM的高MH,则∠MHB=∠MHN=90°,设BH=x,根据勾股定理求出BH,再由勾股定理求出MH,即可求出sin∠MBN;
(3)令y1=-x2+2x+3;y2=mx-m+13,得直线y2=mx-m+13过点(1,13);当y1=y2时,-x2+2x+3=mx-m+13,得出△=m2-36=0,求出m的值,当直线y2=mx-m+13过点C时,m=10,结合图象即可得出m的取值范围.
解:(1)根据题意得:
解得:a=-1,b=2,c=3,
∴抛物线的函数表达式为:y=-x2+2x+3;
(2)存在;理由如下:设直线BC的解析式为y=kx+b,
把B(3,0)、C(0,3)代入得:![]() ,
,
解得:k=-1,b=3,
∴直线BC的解析式为:y=-x+3,
设M(t,-t+3),N(t,-t2+2t+3),
则MN=(-t2+2t+3)-(-t+3)=-t2+3t=-(t-![]() )2+
)2+![]() ;
;
∵-1<0,
∴MN由最大值,
当t=![]() 时,MN的最大值为
时,MN的最大值为![]() ;
;
此时M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),
),
∴MN=![]() -
-![]() =
=![]() ,
,
∵B(3,0)、C(0,3),
∴OB=OC=3,
∵∠BOC=90°,
∴∠OBC=45°,
延长NM交OB于E,如图1所示:
则ME⊥OB,
∴△BME为等腰直角三角形,
∴∠MBE=45°,
∵BE=3-![]() =
=![]() ,
,
∴BM=![]() BE=
BE=![]() ;
;
BN=![]() =
=![]() =
=![]() ;
;
过点M作△BNM的高MH,则∠MHB=∠MHN=90°,
∵MH2=BM2-BH2=MN2-NH2,
设BH=x,则NH=![]() -x,
-x,
∴(![]() )2-x2=(
)2-x2=(![]() )2-(
)2-(![]() -x)2,
-x)2,
解得:x=![]() ,
,
∴BH=![]() ,
,
∴MH=![]() =
=![]() ;
;
∴sin∠MBN=![]() =
=![]() ;
;

(3)令y1=-x2+2x+3;y2=mx-m+13,
∵x=1时,y2=13,
∴直线y2=mx-m+13过点(1,13),
当y1=y2时,-x2+2x+3=mx-m+13,
整理得:x2+(m-2)x-m+10=0,
△=(m-2)2-4×1×(-m+10)=m2-36=0,
解得:m=-6,或m=6,
当直线y2=mx-m+13过点C时,m=10,
由图象可知(如图2所示),
当-6≤m≤10时,均有y1≤y2,

∴m的取值范围为:-6≤m≤10.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
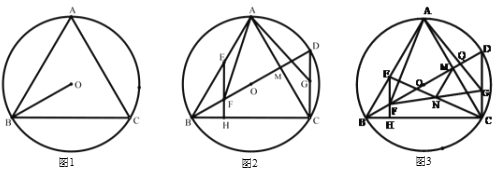
【题目】已知:![]() 内接于
内接于![]() ,
,![]() ,
,![]() 平分
平分![]() .
.
(1)如图,求证:![]() 为等边三角形.
为等边三角形.
(2)如图,![]() 为
为![]() 直径,点
直径,点![]() 在
在![]() 上,
上,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转使点
逆时针旋转使点![]() 落在
落在![]() 上的点
上的点![]() 处,求证:
处,求证:![]() ;
;
(3)如图,在(2)的条件下,![]() 与
与![]() 交于点
交于点![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,若
,若![]() 的面积
的面积![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
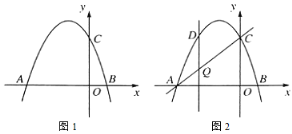
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)求抛物线的函数表达式;
(2)若点![]() 在抛物线上,且
在抛物线上,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图,设点![]() 是线段
是线段![]() 上的一动点,作
上的一动点,作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,求线段
,求线段![]() 长度的最大值,并求出
长度的最大值,并求出![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若正整数a,b,c(a<b<c)满足a2+b2=c2,则称(a,b,c)为一组“勾股数”.
观察下列两类“勾股数”:
第一类(a是奇数):(3,4,5);(5,12,13);(7,24,25);…
第二类(a是偶数):(6,8,10);(8,15,17);(10,24,26);…
(1)请再写出两组勾股数,每类各写一组;
(2)分别就a为奇数、偶数两种情形,用a表示b和c,并选择其中一种情形证明(a,b,c)是“勾股数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
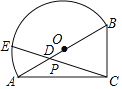
【题目】如图,一块∠BAC为30°的直角三角板ABC的斜边AB与量角器的直径恰好重合,点E在量角器的圆弧边缘处从A到B运动,连接CE,交直径AB于点D.
(1)当点E在量角器上对应的刻度是90°时,则∠ADE的度数为______;
(2)若AB=8,P为CE的中点,当点E从A到B的运动过程中,点P也随着运动,则点P所走过的路线长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
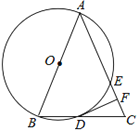
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,请直接写出弧AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 方程![]() =-3必有实数根
=-3必有实数根
B. 若移动函数图象使其经过原点,则只能将图像向右移动1个单位
C. 若k>0,则当x>0时,必有y随着x的增大而增大
D. 若k<0,则当x<-1时,必有y随着x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O在BC边上,以OC为半径作⊙O,与AB切于点D,与边BC,AC分别交于点E,F,且弧DE=弧DF.
(1)求证:△ABC是直角三角形.
(2)连结CD交OF于点P,当cos∠B=![]() 时,求
时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料
计算:(1﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() )﹣(1﹣
)﹣(1﹣![]() ﹣
﹣![]() )(
)(![]() +
+![]() ),令
),令![]() +
+![]() =t,则:
=t,则:
原式=(1﹣t)(t+![]() )﹣(1﹣t﹣
)﹣(1﹣t﹣![]() )t=t+
)t=t+![]() ﹣t2﹣
﹣t2﹣![]() +t2=
+t2=![]()
在上面的问题中,用一个字母代表式子中的某一部分,能达到简化计算的目的,这种思想方法叫做“换元法”,请用“换元法”解决下列问题:
(1)计算:(1﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() )﹣(1﹣
)﹣(1﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() )
)
(2)因式分解:(a2﹣5a+3)(a2﹣5a+7)+4
(3)解方程:(x2+4x+1)(x2+4x+3)=3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com