
【题目】某市粮店出售某种大米,上半月的售价为每公斤![]() 元,下半月的售价为每公斤
元,下半月的售价为每公斤![]() 元.有一餐饮业老板每个月要向该店采购两次大米,且上半月购买一次,下半月购买一次.该老板结合市场米价情况,设计两套采购方案:A.每次购买100公斤大米;B.每次购买100元钱的大米.请你运用所学知识分析一下,该老板采用哪种方式购买较划算.
元.有一餐饮业老板每个月要向该店采购两次大米,且上半月购买一次,下半月购买一次.该老板结合市场米价情况,设计两套采购方案:A.每次购买100公斤大米;B.每次购买100元钱的大米.请你运用所学知识分析一下,该老板采用哪种方式购买较划算.
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
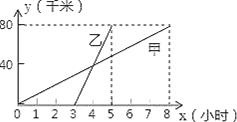
【题目】甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示,请根据图象回答下列问题:
(1)甲先出发______小时后,乙才出发;大约在甲出发______小时后,两人相遇,这时他们离A地_______千米.
(2)两人的行驶速度分别是多少?
(3)分别写出表示甲、乙的路程y(千米)与时间x(小时)之间的函数表达式(不要求写出自变量的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95°.求:∠DCE和∠DCA的度数.

请将以下解答补充完整,
解:因为∠DAB+∠D=180°
所以DC∥AB__________
所以∠DCE=∠B__________
又因为∠B=95°,
所以∠DCE=________°;
因为AC平分∠DAB,∠CAD=25°,根据角平分线定义,
所以∠CAB=________=________°,
因为DC∥AB
所以∠DCA=∠CAB,__________
所以∠DCA=________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线EF∥GH,点A、C在直线EF上,点B在直线GH上,连接AB、BC,∠ACB=50°,∠BAC=30°,BP平分∠ABH,CM平分∠BCF,BP与CM的反向延长线相交于P.
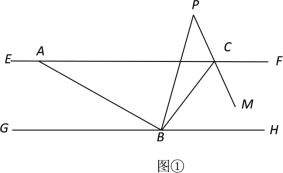
(1)求∠BPC的度数;
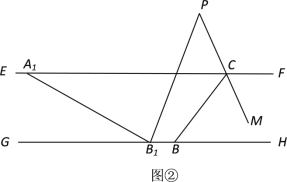
(2)若将图①中的线段AB沿EF向左平移到A1B1,如图②所示位置,此时B1P平分∠A1B1H,CM平分∠BCF,B1P与CM的反向延长线相交于P,求∠B1PC的度数.
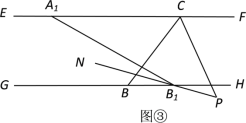
(3)若将图①中的线段AB沿EF向右平移到A1B1,如图③所示位置,此时B1N平分∠A1B1B,CP平分∠BCF, CP与B1N的反向延长线相交于P,求∠B1PC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ![]() ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.

(1)求证:四边形AFCE是平行四边形.
(2)若去掉已知条件的“∠DAB=60°,上述的结论还成立吗 ”若成立,请写出证明过程;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化,促进学生全面发展.我市某区教育局在全区中小学开展“书法、武术、黄梅戏进校园”活动。今年3月份,该区某校举行了“黄梅戏”演唱比赛,比赛成绩评定为A,B,C,D,E五个等级,该校部分学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图,请根据图中信息,解答下列问题.

(1)求该校参加本次“黄梅戏”演唱比赛的学生人数;
(2)求扇形统计图B等级所对应扇形的圆心角度数;
(3)已知A等级的4名学生中有1名男生,3名女生,现从中任意选取2名学生作为全校训练的示范者,请你用列表法或画树状图的方法,求出恰好选1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
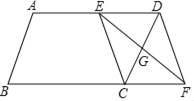
【题目】如图,平行四边形ABCD中,AB=4cm,BC=6cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①AE为何值时四边形CEDF是矩形?为什么?
②AE为何值时四边形CEDF是菱形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
对于任意一个三位数正整数n,如果n的各个数位上的数字互不相同,且都不为零,那么称这个数为“陌生数”,将一个“陌生数”的三个数位上的数字交换顺序,可以得到5个不同的新“陌生数”,把这6个陌生数的和与111的商记为M(n).例如n=123,可以得到132.213.231.312.321这5个新的“陌生数”,这6个“陌生数”的和为123+132+213+231+312+321=1332,因为![]() ,所以M(123)=12.
,所以M(123)=12.
(1)计算:M(125)和M(361)的值;
(2)设s和t都是“陌生数”,其中4和2分别是s的十位和个位上的数字,2和5分别是t的百位和个位上的数字,且t的十位上的数字比s的百位上的数字小2;规定:![]() .若
.若![]() ,则k的值是多少?
,则k的值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com