
【题目】某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)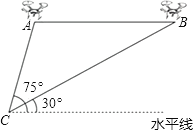
【答案】解:如图,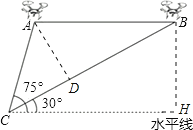
作AD⊥BC,BH⊥水平线,
由题意得:∠ACH=75°,∠BCH=30°,AB∥CH,
∴∠ABC=30°,∠ACB=45°,
∵AB=32m,
∴AD=CD=ABsin30°=16m,BD=ABcos30°=16 ![]() m,
m,
∴BC=CD+BD=(16+16 ![]() )m,
)m,
则BH=BCsin30°=(8+8 ![]() )m
)m
【解析】如图,作AD⊥BC,BH⊥水平线,根据题意确定出∠ABC与∠ACB的度数,利用锐角三角函数定义求出AD与BD的长,由CD+BD求出BC的长,即可求出BH的长. 此题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.
【考点精析】通过灵活运用关于仰角俯角问题,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角即可以解答此题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( ) 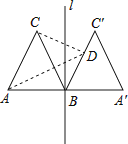
A.4
B.3 ![]()
C.2 ![]()
D.2+ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQAC,
其中正确的结论的个数是( )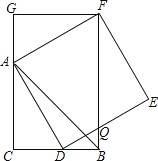
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x﹣3与x轴交于A、B两点,且B(1,0)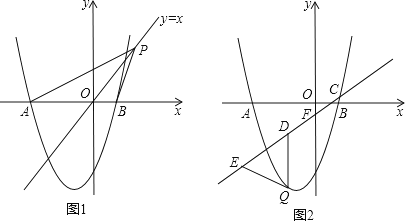
(1)求抛物线的解析式和点A的坐标;
(2)如图1,点P是直线y=x上的动点,当直线y=x平分∠APB时,求点P的坐标;
(3)如图2,已知直线y= ![]() x﹣
x﹣ ![]() 分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A( ![]() ,0),B(0,2),则点B2017的坐标为 .
,0),B(0,2),则点B2017的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2+bx﹣1.
(1)若两点P(﹣3,m)和Q(1,m)在该函数图象上.求b、m的值;
(2)设该函数的顶点为点B,求出点B 的坐标并求三角形BPQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题引入:
(1)如图①所示,△ABC中,点O是∠ABC和∠ACB的平分线的交点,若∠A=![]() ,
,
则∠BOC= (用![]() 表示);不用说明理由,直接填空.
表示);不用说明理由,直接填空.
如图②所示,![]() ,
,![]() ,若
,若![]() ,
,
则∠BOC= (用![]() 表示). 不用说明理由,直接填空.
表示). 不用说明理由,直接填空.

(2)如图③所示,![]() ,
,![]() ,若
,若![]() ,
,
则∠BOC= (用![]() 表示),填空并说明理由.
表示),填空并说明理由.
类比研究:
(3)BO,CO分别是△ABC的外角∠DBC,∠ECB的n等分线,
它们交于点O,![]() ,
,![]() ,若
,若![]() ,
,
则![]() (用
(用![]() 和n表示).不用说明理由,直接填空.
和n表示).不用说明理由,直接填空.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com