
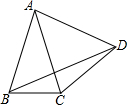
 如图,△ABC中,AB=AC,∠BAC=50°,边AB绕点A逆时针旋转m°,(0<m<360)得到线段AD,连接BD、DC.若△BDC为等腰三角形,则m所有可能的取值是25或100或205或310.
如图,△ABC中,AB=AC,∠BAC=50°,边AB绕点A逆时针旋转m°,(0<m<360)得到线段AD,连接BD、DC.若△BDC为等腰三角形,则m所有可能的取值是25或100或205或310. 分析 构造以A为圆心,以AB为半径的圆,然后根据画出符合题意的图形,然后利用圆周角定理求解即可.
解答 解:∵AB=AC=AD,
∴点C、B、D在以A为圆心,以AB为半径的圆上.
①如图1所示:构造以A为圆心,以AB为半径的圆.
∵BD=DC,
∴∠BAD=∠CAD=$\frac{1}{2}∠BAC=\frac{1}{2}×50°=25°$.
∴m=25.
②如图②所示:构造以A为圆心,以AB为半径的圆.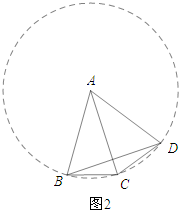
∵BC=CD,
∴∠BAC=∠CAD=50°.
∴∠BAD=100°.
∴m=100.
③如图③所示:构造以A为圆心,以AB为半径的圆.
∵BD=CD,
∴∠BAD=∠CAD=$\frac{1}{2}$(360°-50°)=155°.
∴∠BAC+∠CAD=50°+155°=205.
∴m=205.
④如图④所示:构造以A为圆心,以AB为半径的圆.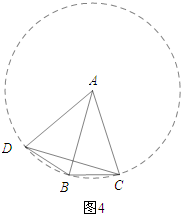
∵BD=BC,
∴∠DAB=∠BAC=50°.
∴m=360°-50°=310.
综上所述,m的值为25或100或205或310.
故答案为:25或100或205或310.
点评 本题主要考查的是圆周角定理、旋转的性质的应用,构造以A为圆心,以AB为半径的圆是解题的关键.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明和爸爸从家一起出发,沿相同的路线以相同的速度步行去体育馆看球赛,途中发现忘带球票,小明立即以更快的速度跑步返回家取票,爸爸继续以原来的速度步行前往体育馆.小明上楼取票用了几分钟后骑自行车沿原来的路线骑向体育馆,小明追上爸爸后用自行车带着爸爸一起前往体育馆,自行车的速度是步行速度的3倍.如图是小明和爸爸距体育馆的路程y(米)与出发的时间x(分)的函数关系.根据图象解答下列问题:
小明和爸爸从家一起出发,沿相同的路线以相同的速度步行去体育馆看球赛,途中发现忘带球票,小明立即以更快的速度跑步返回家取票,爸爸继续以原来的速度步行前往体育馆.小明上楼取票用了几分钟后骑自行车沿原来的路线骑向体育馆,小明追上爸爸后用自行车带着爸爸一起前往体育馆,自行车的速度是步行速度的3倍.如图是小明和爸爸距体育馆的路程y(米)与出发的时间x(分)的函数关系.根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
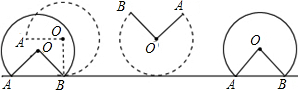
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com