
【题目】如图,已知抛物线y= ![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC//x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC//x轴,点P是直线AC下方抛物线上的动点.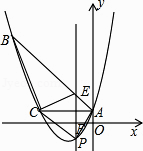
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
【答案】
(1)
解:∵点A(0,1).B(﹣9,10)在抛物线上,
∴ 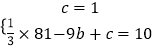 ,
,
∴ ![]() ,
,
∴抛物线的解析式为y= ![]() x2+2x+1
x2+2x+1
(2)
解:∵AC//x轴,A(0,1)
∴ ![]() x2+2x+1=1,
x2+2x+1=1,
∴x1=﹣6,x2=0,
∴点C的坐标(﹣6,1),
∵点A(0,1).B(﹣9,10),
∴直线AB的解析式为y=﹣x+1,
设点P(m, ![]() m2+2m+1)
m2+2m+1)
∴E(m,﹣m+1)
∴PE=﹣m+1﹣( ![]() m2+2m+1)=﹣
m2+2m+1)=﹣ ![]() m2﹣3m,
m2﹣3m,
∵AC⊥EP,AC=6,
∴S四边形AECP
=S△AEC+S△APC
= ![]() AC×EF+
AC×EF+ ![]() AC×PF
AC×PF
= ![]() AC×(EF+PF)
AC×(EF+PF)
= ![]() AC×PE
AC×PE
= ![]() ×6×(﹣
×6×(﹣ ![]() m2﹣3m)
m2﹣3m)
=﹣m2﹣9m
=﹣(m+ ![]() )2+
)2+ ![]() ,
,
∵﹣6<m<0
∴当m=﹣ ![]() 时,四边形AECP的面积的最大值是
时,四边形AECP的面积的最大值是 ![]() ,
,
此时点P(﹣ ![]() ,﹣
,﹣ ![]() )
)
(3)
解:∵y= ![]() x2+2x+1=
x2+2x+1= ![]() (x+3)2﹣2,
(x+3)2﹣2,
∴P(﹣3,﹣2),
∴PF=yF﹣yP=3,CF=xF﹣xC=3,
∴PF=CF,
∴∠PCF=45°
同理可得:∠EAF=45°,
∴∠PCF=∠EAF,
∴在直线AC上存在满足条件的Q,
设Q(t,1)且AB=9 ![]() ,AC=6,CP=3
,AC=6,CP=3 ![]()
∵以C、P、Q为顶点的三角形与△ABC相似,
①当△CPQ∽△ABC时,
∴ ![]() ,
,
∴ ![]() ,
,
∴t=﹣4或t=﹣8(不符合题意,舍)
∴Q(﹣4,1)
②当△CQP∽△ABC时,
∴ ![]() ,
,
∴ ![]() ,
,
∴t=3或t=﹣15(不符合题意,舍)
∴Q(3,1)
【解析】(1)用待定系数法求出抛物线解析式即可;(2)设点P(m, ![]() m2+2m+1),表示出PE=﹣
m2+2m+1),表示出PE=﹣ ![]() m2﹣3m,再用S四边形AECP=S△AEC+S△APC=
m2﹣3m,再用S四边形AECP=S△AEC+S△APC= ![]() AC×PE,建立函数关系式,求出极值即可;(3)先判断出PF=CF,再得到∠PCA=∠EAC,以C、P、Q为顶点的三角形与△ABC相似,分两种情况计算即可.
AC×PE,建立函数关系式,求出极值即可;(3)先判断出PF=CF,再得到∠PCA=∠EAC,以C、P、Q为顶点的三角形与△ABC相似,分两种情况计算即可.
【考点精析】通过灵活运用相似三角形的应用,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.P是直径MN上一动点,则PA+PB的最小值为( )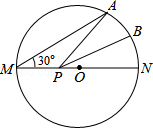
A.![]()
B.1
C.2
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
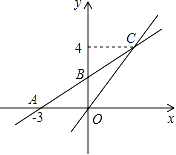
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(﹣3,0),与y轴交点为B,且与正比例函数y=![]() x的图象交于点C(m,4).
x的图象交于点C(m,4).
(1)求m的值及一次函数y=kx+b的表达式;
(2)观察函数图象,直接写出关于x的不等式![]() x<kx+b的解集.
x<kx+b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;其中正确的结论有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OP平分∠BOA,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论中错误的是( )

A. PC=PD B. OC=OD C. OC=OP D. ∠CPO=∠DPO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据.
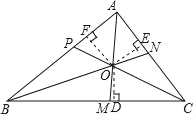
已知:如图,AM,BN,CP是△ABC的三条角平分线.
求证:AM、BN、CP交于一点.
证明:如图,设AM,BN交于点O,过点O分别作OD⊥BC,OF⊥AB,垂足分别为点D,E,F.
∵O是∠BAC角平分线AM上的一点( ),
∴OE=OF( ).
同理,OD=OF.
∴OD=OE( ).
∵CP是∠ACB的平分线( ),
∴O在CP上( ).
因此,AM,BN,CP交于一点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善生态环境,防止水土流失,某村计划在江汉堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:
甲林场 | 乙林场 | ||
购树苗数量 | 销售单价 | 购树苗数量 | 销售单价 |
不超过1000棵时 | 4元/棵 | 不超过2000棵时 | 4元/棵 |
超过1000棵的部分 | 3.8元/棵 | 超过2000棵的部分 | 3.6元/棵 |
设购买白杨树苗x棵,到两家林场购买所需费用分别为y甲(元)、y乙(元).
(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为元,若都在乙林场购买所需费用为元;
(2)分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
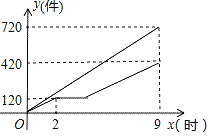
【题目】甲、乙两车间同时开始加工一批零件,从开始加工到加工完这批零件,甲车间工作了9小时,乙车间在中途停工一段时间维修设备,修好后马上按停工前的工作效率继续加工,直到与甲车间同时完成这批零件的加工任务为止,设甲、乙两车间各自加工零件的数量为y(个),甲车间加工的时间为x(时),y与x之间的函数图象如图所示,下列说法其中正确的个数为( )
①这批零件的总个数为1260个;
②甲车间每小时加工零件个数为80个;
③乙车间维修设备后,乙车间加工零件数量y与x之间的函数关系式y=60x﹣120;
④乙车间维修设备用了2个小时
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com