
ЁОЬтФПЁПШчЭМЃЌЩфЯпANЩЯгавЛЕуBЃЌABЃН5ЃЌtanЁЯMANЃН![]() ЃЌЕуCДгЕуAГіЗЂвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШбиЩфЯпANдЫЖЏЃЌЙ§ЕуCзїCDЁЭANНЛЩфЯпAMгкЕуDЃЌдкЩфЯпCDЩЯШЁЕуFЃЌЪЙЕУCFЃНCBЃЌСЌНсAFЃЎЩшЕуCЕФдЫЖЏЪБМфЪЧtЃЈУыЃЉЃЈtЃО0ЃЉЃЎ
ЃЌЕуCДгЕуAГіЗЂвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШбиЩфЯпANдЫЖЏЃЌЙ§ЕуCзїCDЁЭANНЛЩфЯпAMгкЕуDЃЌдкЩфЯпCDЩЯШЁЕуFЃЌЪЙЕУCFЃНCBЃЌСЌНсAFЃЎЩшЕуCЕФдЫЖЏЪБМфЪЧtЃЈУыЃЉЃЈtЃО0ЃЉЃЎ
ЃЈ1ЃЉЕБЕуCдкЕуBгвВрЪБЃЌЧѓADЁЂDFЕФГЄЃЎЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉСЌНсBDЃЌЩшЁїBCDЕФУцЛ§ЮЊSЦНЗНЕЅЮЛЃЌЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ3ЃЉЕБЁїAFDЪЧжсЖдГЦЭМаЮЪБЃЌжБНгаДГіtЕФжЕЃЎ

ЁОД№АИЁПЃЈ1ЃЉADЃН5tЃЌDF=t+5ЃЎЃЈ2ЃЉЕБ0ЃМtЃМ![]() ЪБЃЌSЃНЉ6t2+10tЃЎЕБtЃО
ЪБЃЌSЃНЉ6t2+10tЃЎЕБtЃО![]() ЪБЃЌSЃН6t2Љ10tЃЎЃЈ3ЃЉtЕФжЕЮЊ
ЪБЃЌSЃН6t2Љ10tЃЎЃЈ3ЃЉtЕФжЕЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
(1)РћгУЙДЙЩЖЈРэЫуГіAD,БэЪОГіCB,МДПЩБэЪОГіDF.
(2)ЗжБ№ЬжТл0ЃМtЃМ![]() ЪБКЭtЃО
ЪБКЭtЃО![]() ЪБ,РћгУУцЛ§ЙЋЪНМЦЫуМДПЩ.
ЪБ,РћгУУцЛ§ЙЋЪНМЦЫуМДПЩ.
(3)ЗжБ№ЬжТлЕБDFЃНADЪБЕФвЛжжЧщПіЁЂЕБAFЃНDFЪБЕФСНжжЧщПі.
НтЃКЃЈ1ЃЉдкRtЁїACDжаЃЌACЃН3tЃЌtanЁЯMANЃН![]() ЃЌ
ЃЌ
ЁрCDЃН4tЃЎ
ЁрADЃН![]() ЃЌ
ЃЌ
ЕБЕуCдкЕуBгвВрЪБЃЌCBЃН3tЉ5ЃЌ
ЁрCFЃНCBЃЎ
ЁрDFЃН4tЉЃЈ3tЉ5ЃЉЃНt+5ЃЎ
ЃЈ2ЃЉЕБ0ЃМtЃМ![]() ЪБЃЌSЃН
ЪБЃЌSЃН![]() ЃЈ5Љ3tЃЉ4tЃНЉ6t2+10tЃЎ
ЃЈ5Љ3tЃЉ4tЃНЉ6t2+10tЃЎ
ЕБtЃО![]() ЪБЃЌSЃН
ЪБЃЌSЃН![]() ЃЈ3tЉ5ЃЉ4tЃН6t2Љ10tЃЎ
ЃЈ3tЉ5ЃЉ4tЃН6t2Љ10tЃЎ
ЃЈ3ЃЉЂйШчЭМ1жаЃЌЕБDFЃНADЪБЃЌЁїADFЪЧжсЖдГЦЭМаЮЃЎ
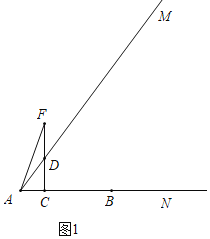
дђга5Љ3tЉ4tЃН5tЃЌНтЕУtЃН![]() ЃЌ
ЃЌ
ЂкШчЭМ2жаЃЌЕБAFЃНDFЪБЃЌЁїADFЪЧжсЖдГЦЭМаЮЃЎ

зїFHЁЭADЃЎ
ЁпFAЃНDFЃЌ
ЁрAHЃНDHЃН![]() tЃЌ
tЃЌ
гЩcosЁЯFDHЃН![]() ЃЌПЩЕУ
ЃЌПЩЕУ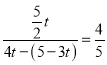 ЃЌНтЕУtЃН
ЃЌНтЕУtЃН![]() ЃЎ
ЃЎ
ЂлШчЭМ3жаЃЌЕБAFЃНDFЪБЃЌЁїADFЪЧжсЖдГЦЭМаЮЃЎ
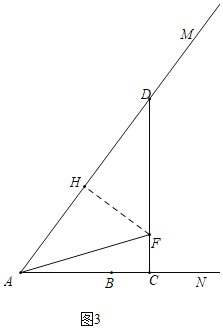
зїFHЁЭADЃЎ
ЁпFAЃНDFЃЌ
ЁрAHЃНDHЃН![]() tЃЌ
tЃЌ
гЩcosЁЯFDHЃН![]() ЃЌПЩЕУ
ЃЌПЩЕУ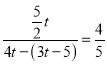 ЃЌНтЕУtЃН
ЃЌНтЕУtЃН![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФtЕФжЕЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ


 ПкЫуаФЫуЫйЫугІгУЬтЯЕСаД№АИ
ПкЫуаФЫуЫйЫугІгУЬтЯЕСаД№АИ ЭЌВНЭиеЙдФЖСЯЕСаД№АИ
ЭЌВНЭиеЙдФЖСЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЙЫъЧЎгЩРДвбОУЃЌЙХГЦЁАбсЪЄЧЎЁБЁЂЁАбЙЫюЧЎЁБЕШЃЎюѕюѕЭЌбЇдк2019ФъДКНкЙВЪеЕН10ЮЛГЄБВИјЕФбЙЫъЧЎЃЌЗжБ№ЪЧЃК100дЊЁЂ200дЊЁЂ100дЊЁЂ50дЊЁЂ400дЊЁЂ300дЊЁЂ50дЊЁЂ100дЊЁЂ200дЊЁЂ400дЊЃЎЙигкетзщЪ§ОнЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A.жаЮЛЪ§ЪЧ200дЊB.жкЪ§ЪЧ100дЊ
C.ЦНОљЪ§ЪЧ200дЊD.МЋВюЪЧ300дЊ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшa,bЪЧШЮвтСНИіВЛЕШЪЕЪ§ЃЌЮвУЧЙцЖЈЃКТњзуВЛЕШЪНaЁмxЁмbЕФЪЕЪ§xЕФЫљгаШЁжЕЕФШЋЬхНазіБеЧјМфЃЌБэЪОЮЊ[a,b]ЃЎЖдгквЛИіКЏЪ§ЃЌШчЙћЫќЕФздБфСПxгыКЏЪ§жЕyТњзуЃКЕБmЁмxЁмnЪБЃЌгаmЁмyЁмn,ЮвУЧОЭГЦДЫКЏЪ§ЪЧБеЧјМф[m.n]ЩЯЕФЁАБеКЏЪ§ЁБЃЎШчКЏЪ§![]() ЃЌЕБx=1ЪБЃЌy=3ЃЛЕБx=3ЪБЃЌy=1ЃЌМДЕБ
ЃЌЕБx=1ЪБЃЌy=3ЃЛЕБx=3ЪБЃЌy=1ЃЌМДЕБ![]() ЪБЃЌга
ЪБЃЌга![]() ЃЌЫљвдЫЕКЏЪ§
ЃЌЫљвдЫЕКЏЪ§![]() ЪЧБеЧјМф[1,3]ЩЯЕФЁАБеКЏЪ§ЁБЃЎ
ЪЧБеЧјМф[1,3]ЩЯЕФЁАБеКЏЪ§ЁБЃЎ
ЃЈ1ЃЉЗДБШР§КЏЪ§y=![]() ЪЧБеЧјМф[1,2016]ЩЯЕФЁАБеКЏЪ§ЁБТ№ЃПЧыХаЖЯВЂЫЕУїРэгЩЃЛ
ЪЧБеЧјМф[1,2016]ЩЯЕФЁАБеКЏЪ§ЁБТ№ЃПЧыХаЖЯВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєЖўДЮКЏЪ§y=![]() ЪЧБеЧјМф[1,2]ЩЯЕФЁАБеКЏЪ§ЁБЃЌЧѓkЕФжЕЃЛ
ЪЧБеЧјМф[1,2]ЩЯЕФЁАБеКЏЪ§ЁБЃЌЧѓkЕФжЕЃЛ
ЃЈ3ЃЉШєвЛДЮКЏЪ§y=kx+b(kЁй0)ЪЧБеЧјМф[m,n]ЩЯЕФЁАБеКЏЪ§ЁБЃЌЧѓДЫКЏЪ§ЕФБэДяЪНЃЈгУКЌmЃЌnЕФДњЪ§ЪНБэЪОЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСРэНтЃК
ШчЭМЂйЃЌдкЫФБпаЮABCDЕФБпABЩЯШЮШЁвЛЕуEЃЈЕуEВЛгыAЁЂBжиКЯЃЉЃЌЗжБ№СЌНгEDЁЂECЃЌПЩвдАбЫФБпаЮABCDЗжГЩШ§ИіШ§НЧаЮЃЌШчЙћЦфжагаСНИіШ§НЧаЮЯрЫЦЃЌЮвУЧОЭАбEНазіЫФБпаЮABCDЕФБпABЩЯЕФЁАЯрЫЦЕуЁБЃЛШчЙћетШ§ИіШ§НЧаЮЖМЯрЫЦЃЌЮвУЧОЭАбEНазіЫФБпаЮABCDЕФБпABЩЯЕФЁАЧПЯрЫЦЕуЁБЃЎНтОіЮЪЬтЃК
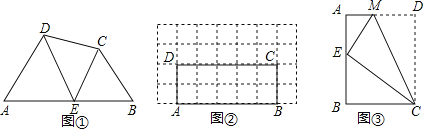
ЃЈ1ЃЉШчЭМЂйЃЌЁЯAЃНЁЯBЃНЁЯDECЃН45ЁуЃЌЪдХаЖЯЕуEЪЧЗёЪЧЫФБпаЮABCDЕФБпABЩЯЕФЯрЫЦЕуЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌдкОиаЮABCDжаЃЌAЁЂBЁЂCЁЂDЫФЕуОљдке§ЗНаЮЭјИёЃЈЭјИёжаУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЃЉЕФИёЕуЃЈМДУПИіаЁе§ЗНаЮЕФЖЅЕуЃЉЩЯЃЌЪддкЭМЂкжаЛГіОиаЮABCDЕФБпABЩЯЕФЧПЯрЫЦЕуЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌНЋОиаЮABCDбиCMелЕўЃЌЪЙЕуDТфдкABБпЩЯЕФЕуEДІЃЌШєЕуEЧЁКУЪЧЫФБпаЮABCMЕФБпABЩЯЕФвЛИіЧПЯрЫЦЕуЃЌЪдШЗЖЈEЕуЮЛжУЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
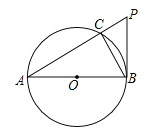
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌPBгыЁбOЯрЧагкЕуBЃЌСЌНгPAНЛЁбOгкЕуCЃЌСЌНгBCЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯBAC=ЁЯCBPЃЛ
ЃЈ2ЃЉЧѓжЄЃКPB2=PCPAЃЛ
ЃЈ3ЃЉЕБAC=6ЃЌCP=3ЪБЃЌЧѓsinЁЯPABЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
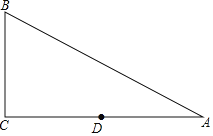
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌACЃН4ЃЌBCЃН3ЃЌЕуDЪЧБпACЕФжаЕуЃЌЕуEЃЌFдкБпABЩЯЃЌЕБЁїDEFЪЧЕШбќШ§НЧаЮЃЌЧвЕзНЧЕФе§ЧажЕЪЧ![]() ЪБЃЌЁїDEFбќГЄЕФжЕЪЧ_____ЃЎ
ЪБЃЌЁїDEFбќГЄЕФжЕЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНax2+bxЉ3НЛxжсгкЕуAЃЈЉ1ЃЌ0ЃЉКЭЕуBЃЈ3ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЌЖЅЕуЪЧDЃЌЖдГЦжсНЛxжсгкЕуEЃЎ
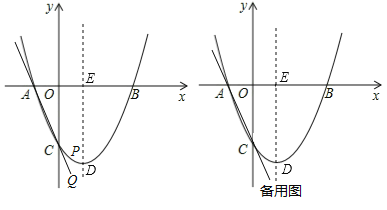
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЪЧХзЮяЯпдкЕкЫФЯѓЯоФкЕФвЛЕуЃЌЙ§ЕуPзїPQЁЮyжсЃЌНЛжБЯпACгкЕуQЃЌЩшЕуPЕФКсзјБъЪЧmЃЎ
ЂйЧѓЯпЖЮPQЕФГЄЖШnЙигкmЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкСЌНгAPЃЌCPЃЌЧѓЕБЁїACPУцЛ§ЮЊ![]() ЪБЕуPЕФзјБъЃЛ
ЪБЕуPЕФзјБъЃЛ
ЃЈ3ЃЉШєЕуNЪЧХзЮяЯпЖдГЦжсЩЯвЛЕуЃЌдђХзЮяЯпЩЯЪЧЗёДцдкЕуMЃЌЪЙЕУвдЕуBЃЌCЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЯпЖЮBNЕФГЄЖШЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаМзЁЂввСНжжПЭГЕЃЌ2СОМзжжПЭГЕгы3СОввжжПЭГЕЕФзмдиПЭСПЮЊ180ШЫЃЌ1СОМзжжПЭГЕгы2СОввжжПЭГЕЕФзмдиПЭСПЮЊ105ШЫЃЎ
ЃЈ1ЃЉЧыЮЪ1СОМзжжПЭГЕгы1СОввжжПЭГЕЕФдиПЭСПЗжБ№ЮЊЖрЩйШЫЃП
ЃЈ2ЃЉФГбЇаЃзщжЏ240УћЪІЩњМЏЬхЭтГіЛюЖЏЃЌФтзтгУМзЁЂввСНжжПЭГЕЙВ6СОЃЌвЛДЮНЋШЋВПЪІЩњЫЭЕНжИЖЈЕиЕуЃЎШєУПСОМзжжПЭГЕЕФзтН№ЮЊ400дЊЃЌУПСОввжжПЭГЕЕФзтН№ЮЊ280дЊЃЌЧыИјГізюНкЪЁЗбгУЕФзтГЕЗНАИЃЌВЂЧѓГізюЕЭЗбгУЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌACЪЧЯвЃЌжБЯпEFОЙ§ЕуCЃЌADЁЭEFгкЕуDЃЌЁЯDAC=ЁЯBAC.

ЃЈ1ЃЉЧѓжЄЃКEFЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЧѓжЄЃКAC2=ADЁЄABЃЛ
ЃЈ3ЃЉШєЁбOЕФАыОЖЮЊ2ЃЌЁЯACD=300ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com