
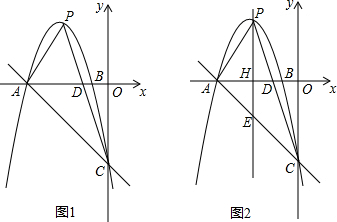
分析 ①如图1根据已知条件得到PB=$\frac{1}{3}$BC=1,根据勾股定理即可得到结论;
②如图2,根据已知条件得到PC=$\frac{1}{3}$BC=1,根据勾股定理即可得到结论.
解答 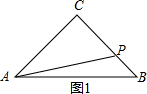 解:①如图1,∵∠ACB=90°,AC=BC=3,
解:①如图1,∵∠ACB=90°,AC=BC=3,
∵PB=$\frac{1}{3}$BC=1,
∴CP=2,
∴AP=$\sqrt{A{C}^{2}+P{C}^{2}}$=$\sqrt{13}$,
②如图2,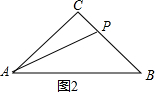 ∵∠ACB=90°,AC=BC=3,
∵∠ACB=90°,AC=BC=3,
∵PC=$\frac{1}{3}$BC=1,
∴AP=$\sqrt{A{C}^{2}+P{C}^{2}}$=$\sqrt{10}$,
综上所述:AP的长为$\sqrt{13}$或$\sqrt{10}$,
故答案为:$\sqrt{13}$或$\sqrt{10}$.
点评 本题考查了等腰直角三角形的性质,勾股定理,熟练掌握等腰直角三角形的性质是解题的关键.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:选择题
| A. | 对角线相等的菱形是正方形 | |
| B. | 对角线互相垂直的矩形是正方形 | |
| C. | 对角线互相垂直且相等的四边形是正方形 | |
| D. | 对角线互相垂直且相等的平行四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
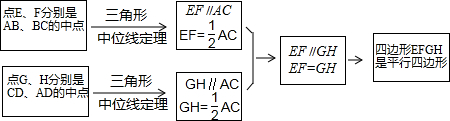
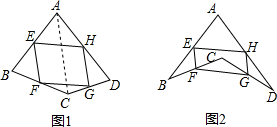
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
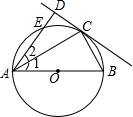 如图,AB为⊙O的直径,点E在⊙O上,C为$\widehat{BE}$的中点,过点C作直线CD⊥AE于D,连接AC、BC.
如图,AB为⊙O的直径,点E在⊙O上,C为$\widehat{BE}$的中点,过点C作直线CD⊥AE于D,连接AC、BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
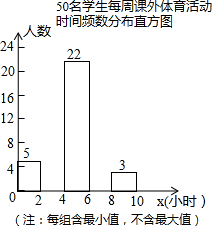 为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:
为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 周末,小芳骑自行车从家出发到野外郊游,从家出发0.5小时到达甲地,游玩一段时间后按原速前往乙地,小芳离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,行驶10分钟时,恰好经过甲地,如图是她们距乙地的路程y(km)与小芳离家时间x(h)的函数图象.
周末,小芳骑自行车从家出发到野外郊游,从家出发0.5小时到达甲地,游玩一段时间后按原速前往乙地,小芳离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,行驶10分钟时,恰好经过甲地,如图是她们距乙地的路程y(km)与小芳离家时间x(h)的函数图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com