
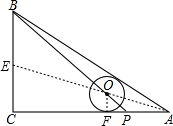
 如图.在△ABC中,∠C=90°,AC=8,AB=10,点P在线段AC上运动,若圆O的半径是y,AP=x,且⊙0的圆心在线段BP上,圆O与AB,AC都相切.请求出y与x的函数关系式.
如图.在△ABC中,∠C=90°,AC=8,AB=10,点P在线段AC上运动,若圆O的半径是y,AP=x,且⊙0的圆心在线段BP上,圆O与AB,AC都相切.请求出y与x的函数关系式.| OF |
| BC |
| PF |
| PC |
| AF |
| AC |
| OF |
| EC |
| AB |
| AC |
| BE |
| CE |
| BE |
| CE |
| 10 |
| 8 |
| 5 |
| 4 |
| CE |
| BC |
| 4 |
| 9 |
| 8 |
| 3 |
| PF |
| PC |
| OF |
| BC |
| AF |
| AC |
| OF |
| CE |
| PF |
| 8-x |
| y |
| 6 |
| x+PF |
| 8 |
| y | ||
|
| 6x |
| 10+x |
| 6x |
| 10+x |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com