
在平面直角坐标系xOy中,已知抛物线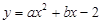 经过(2,1)和(6,-5)两点.
经过(2,1)和(6,-5)两点.
(1)求抛物线的解析式;
(2)设此抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点,点P是在直线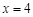 右侧的此抛物线上一点,过点P作PM
右侧的此抛物线上一点,过点P作PM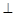
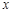 轴,垂足为M. 若以A、P、M为顶点的三角形与△OCB相似,求点P的坐标;
轴,垂足为M. 若以A、P、M为顶点的三角形与△OCB相似,求点P的坐标;
(3)点E是直线BC上的一点,点F是平面内的一点,若要使以点O、B、E、F为顶点的四边形是菱形,请直接写出点F的坐标.
(1)抛物线的解析式为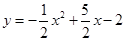
(2)点P的坐标为(8,-14)或(5,-2)
(3)点F的坐标为(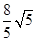 ,
,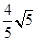 )或(
)或( ,
,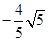 )或(
)或(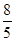 ,
,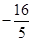 )或(2,1)
)或(2,1)
解析试题分析:(1)由题意,得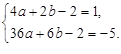
解这个方程组,得 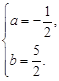 ∴ 抛物线的解析式为
∴ 抛物线的解析式为 .
.
(2)令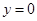 ,得
,得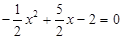 .解这个方程,得
.解这个方程,得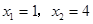 .∴A(1,0),B(4,0),令
.∴A(1,0),B(4,0),令 ,得
,得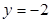 .∴C(0,-2),设P(
.∴C(0,-2),设P(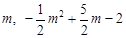 ),因为
),因为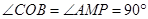 ,①当
,①当 时,△OCB∽△MAP.∴
时,△OCB∽△MAP.∴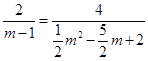 ,解这个方程,得
,解这个方程,得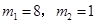 (舍),∴点P的坐标为(8,-14)②当
(舍),∴点P的坐标为(8,-14)②当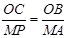 时,△OCB∽△MPA.∴
时,△OCB∽△MPA.∴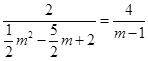 ,解这个方程,得
,解这个方程,得 (舍).∴点P的坐标为(5,-2),∴点P的坐标为(8,-14)或(5,-2)
(舍).∴点P的坐标为(5,-2),∴点P的坐标为(8,-14)或(5,-2)
(3)先由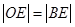 确定点E的几个位置,再由E点确定F点的位置,推出点F的坐标为(
确定点E的几个位置,再由E点确定F点的位置,推出点F的坐标为(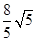 ,
,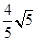 )或(
)或( ,
,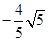 )或(
)或(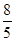 ,
,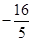 )或(2,1)
)或(2,1)
考点:抛物线解析式的复原,抛物线与集合的简单结合
点评:本题难度一般,学生可以通过方程组的简单计算,求出函数解析式


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com