
【题目】已知在平面直角坐标系中有 A(-2,1), B(3, 1),C(2, 3)三点,请回答下列问题:

(1)在坐标系内描出点A, B, C的位置.
(2)画出![]() 关于直线x=-1对称的
关于直线x=-1对称的![]() ,并写出
,并写出![]() 各点坐标.
各点坐标.
(3)在y轴上是否存在点P,使以A,B, P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标:若不存在,请说明理由.
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,某地准备开荒种树,两次参加活动的人数及开支如下表:
开荒(人) | 种树(人) | 总支出(元) | |
第一次 | 15 | 9 | 57000 |
第二次 | 10 | 16 | 68000 |
(1)若两次开荒种树活动的人均支出费用一样,求开荒和种树的人均支出费用各是多少?
(2)在人均支出费用不变的情况下,为节约开支,施工单位准备抽调40人参加此活动,要使得总支出不超过102 000元,且开荒人数小于种树人数,则有哪几种分配人员方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,等边△ABC中,D、E分别在BC、AC边上运动,且始终保持BD=CE,点D、E始终不与等边△ABC的顶点重合.连接AD、BE,AD、BE交于点F.
(1)写出在运动过程中始终全等的三角形,井选择其中一组证明;
(2)运动过程中,∠BFD的度数是否会改变?如果改变,请说明理由;如果不变,求出∠BFD的度数,再说明理由.
(3)直接写出运动过程中,AE、AB、BD三条线段长度之间的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB的直角边OA在x轴上,顶点B的坐标为(6,8),直线CD交AB于点D(6,3),交x轴于点C(12,0).
(1)求直线CD的函数表达式;
(2)动点P在x轴上从点(﹣10,0)出发,以每秒1个单位的速度向x轴正方向运动,过点P作直线l垂直于x轴,设运动时间为t.
①点P在运动过程中,是否存在某个位置,使得∠PDA=∠B?若存在,请求出点P的坐标;若不存在,请说明理由;
②请探索当t为何值时,在直线l上存在点M,在直线CD上存在点Q,使得以OB为一边,O,B,M,Q为顶点的四边形为菱形,并求出此时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系___;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E分别在AC,AB上.

【1】(1) 已知,BD=CE,CD=BE,求证:AB=AC;
【2】(2) 分别将“BD=CE”记为①,“CD=BE” 记为②,“AB=AC”记为③.添加条件①、③,以②为结论构成命题1,添加条件②、③以①为结论构成命题2.命题1是命题2的 命题,命题2是
命题.(选择“真”或“假”填入空格).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏思考解决如下问题:
原题:如图1,点![]() ,
,![]() 分别在菱形
分别在菱形![]() 的边
的边![]() ,
,![]() 上,
上,![]() ,求证:
,求证:![]() .
.
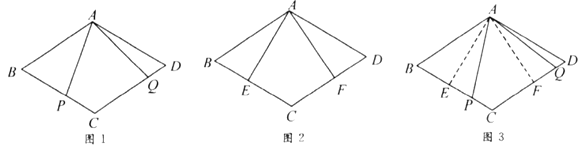
(1)小敏进行探索,若将点![]() ,
,![]() 的位置特殊化:把
的位置特殊化:把![]() 绕点
绕点![]() 旋转得到
旋转得到![]() ,使
,使![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,如图2,此时她证明了
上,如图2,此时她证明了![]() .请你证明.
.请你证明.
(2)受以上(1)的启发,在原题中,添加辅助线:如图3,作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() .请你继续完成原题的证明.
.请你继续完成原题的证明.
(3)如果在原题中添加条件:![]() ,
,![]() ,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).
,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).
查看答案和解析>>
科目:初中数学 来源: 题型:
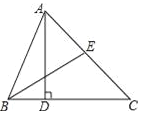
【题目】如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=32°,∠AEB=70°.
(1)求∠CAD的度数;
(2)若点F为线段BC上任意一点,当△EFC为直角三角形时,则∠BEF的度数为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com