
(本题满分10分)
如图所示,在直角坐标系中,平行四边形OABC的顶点坐标B(6,3),C(2,3).
(1)求出过O、A、B三点的抛物线解析式;
(2)若直线![]() 恰好将平行四边形OABC的面积分成相等的两部分,试求b的值
恰好将平行四边形OABC的面积分成相等的两部分,试求b的值
(3)若![]() 与
与![]() 轴、y轴的交点分别记为M、N,(1)中抛物线的对称轴与此抛物
轴、y轴的交点分别记为M、N,(1)中抛物线的对称轴与此抛物
线及![]() 轴的交点分别记作点D、点E,试判断△OMN与△OED是否相似?
轴的交点分别记作点D、点E,试判断△OMN与△OED是否相似?
(1)如图,分别过点C、B作CF⊥![]() 轴、BH⊥
轴、BH⊥![]() 轴,垂足分别为点F、点H,
轴,垂足分别为点F、点H,
则四边形CFHB为矩形,已知B(6,3),C(2,3),
则AH=OF=2,OH=6,可得OA=OH-AH=6-2=4.故点A的坐标为(4,0).
设抛物线解析式为![]() ,由于抛物线过三点A(4,0),B(6,3),O(0,0)则有
,由于抛物线过三点A(4,0),B(6,3),O(0,0)则有
 解之得
解之得
故其解析式为![]() … …3分
… …3分
(2)如图,连接OB,取OB的中点P,作PQ⊥![]() 轴,则PQ=
轴,则PQ=![]() BH=
BH=![]() ,OQ=
,OQ=![]() OH=3,
OH=3,
所以点P的坐标为(3,![]() )…………………………………………………4分
)…………………………………………………4分
过点P的直线一定会平分平行四边形OABC的面积,
因此直线![]() 过点P即可.………5分
过点P即可.………5分
故有![]() =-
=-![]() ×3+b,解之得b =3.……………………………………………6分
×3+b,解之得b =3.……………………………………………6分
(3)答:它们相似.…………………………………………………………7分
易知M、N的坐标分别为(6,0)、(0,3);
点D、点E的坐标分别为(2,-1)、(2,0) …8分
可知线段OM=6,ON=3,OE=2,DE=1,
在△OMN与△ODE中
∵![]()
∴![]()
又∠MON=∠OED,
∴△OMN∽△OED. ………………………10分
解析:略


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
(本题满分10分)
如图,将OA = 6,AB = 4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.

(1)点B的坐标为 ;用含t的式子表示点P的坐标为 ;(3分)
(2)记△OMP的面积为S,求S与t的函数关系式(0 < t < 6);并求t为何值时,S有最大值?(4分)
(3)试探究:当S有最大值时,在y轴上是否存在点T,使直线MT把△ONC分割成三角形和四边形两部分,且三角形的面积是△ONC面积的?若存在,求出点T的坐标;若不存在,请说明理由.(3分)
查看答案和解析>>
科目:初中数学 来源: 题型:
 的图象的顶点为
的图象的顶点为 .二次函数
.二次函数 的图象与
的图象与 轴交于原点
轴交于原点 及另一点
及另一点 ,它的顶点
,它的顶点 在函数
在函数 的图象的对称轴上.
的图象的对称轴上.
 与点
与点 的坐标;
的坐标; 为菱形时,求函数
为菱形时,求函数 的关系式.
的关系式.查看答案和解析>>
科目:初中数学 来源: 题型:
 与支架
与支架 所在直线相交于水箱横断面
所在直线相交于水箱横断面 的圆心
的圆心 ,支架
,支架 与水平面
与水平面 垂直,
垂直, 厘米,
厘米,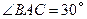 ,另一根辅助支架
,另一根辅助支架 厘米,
厘米, .
. 的长度;(结果保留根号)
的长度;(结果保留根号) 的长度.(结果保留三个有效数字,参考数据:
的长度.(结果保留三个有效数字,参考数据: )
)

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011年江苏省泰州市中考数学试卷 题型:解答题
(本题满分10分)如图,以点O为圆心的两个同心圆中,矩形ABCD的边BC为大圆的弦,边AD与小圆相切于点M,OM的延长线与BC相交于点N。
(1)点N是线段BC的中点吗?为什么?
(2)若圆环的宽度(两圆半径之差)为6cm,AB=5cm,BC=10cm,求小圆的半径。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com