
 如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:
如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
分析 ①如图1,根据正方形边长求DE的长,由折叠得:AD=AF=3,DE=EF=1,根据HL证明Rt△ABG≌Rt△AFG,BG=FG,设BG=x,在直角△EGC中利用勾股定理列方程求出x的值,比较BG和CG的大小;
②如图2,作辅助线,根据平行线分线段成比例定理列式求FH和GH的长,根据勾股定理求FC,发现FG≠FC;
③如图1,根据正方形的内角为90°,及∠DAE=∠FAE,∠BAG=∠FAG,得∠GAE=45°.
解答 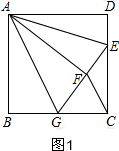 解:①如图1,∵四边形ABCD是正方形,
解:①如图1,∵四边形ABCD是正方形,
∴CD=AB=3,
∵CD=3DE,
∴DE=1,
∴CE=2,
由折叠得:DE=EF=1,AD=AF=3,
∴AB=AF,
∵∠B=∠AFG=90°,AG=AG,
∴Rt△ABG≌Rt△AFG,
∴BG=FG,
设BG=x,则CG=3-x,FG=x,
由勾股定理得:EG2=CG2+EC2,
(x+1)2=22+(3-x)2,
解得:x=$\frac{3}{2}$,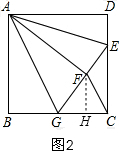
∴BG=$\frac{3}{2}$,
∴CG=3-$\frac{3}{2}$=$\frac{3}{2}$,
∴点G是BC的中点;
所以①正确;
②如图2,过F作FH⊥BC于H,
∵FH∥DC,
∴$\frac{FH}{EC}=\frac{GF}{GE}=\frac{GH}{GC}$,
∴$\frac{FH}{2}=\frac{\frac{3}{2}}{1+\frac{3}{2}}$=$\frac{GH}{\frac{3}{2}}$,
∴FH=$\frac{6}{5}$,GH=$\frac{9}{10}$,
∴CH=$\frac{3}{2}$-$\frac{9}{10}$=$\frac{3}{5}$,
∴FC=$\sqrt{(\frac{6}{5})^{2}+(\frac{3}{5})^{2}}$=$\frac{3\sqrt{5}}{5}$,
由①得FG=BG=$\frac{3}{2}$,
∴FG≠FC,
所以②不正确;
③如图1,∵∠DAE=∠FAE,∠BAG=∠FAG,
∴∠BAG+∠DAE=∠FAG+∠FAE,
∵∠DAB=90°,
∴∠EAG=$\frac{1}{2}$∠DAB=45°,
所以③正确;
故结论正确的是:①③,
故选B.
点评 本题考查了正方形和折叠的性质,明确折叠前后的对应角相等,正方形的四边相等且四个角都是直角;利用勾股定理列方程求边的长度,恰当地作辅助线,构建平行线,根据平行线分线段成比例定理列比例式求边长;从而比较边的大小关系.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案科目:初中数学 来源: 题型:解答题
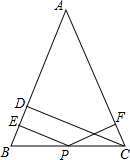 如图,在△ABC中,AB=AC,CD⊥AB于D,P为BC上的任意一点,过P点分别作PE⊥AB,PF⊥CA,垂足分别为E,F,则有PE+PF=CD,你能说明为什么吗?
如图,在△ABC中,AB=AC,CD⊥AB于D,P为BC上的任意一点,过P点分别作PE⊥AB,PF⊥CA,垂足分别为E,F,则有PE+PF=CD,你能说明为什么吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
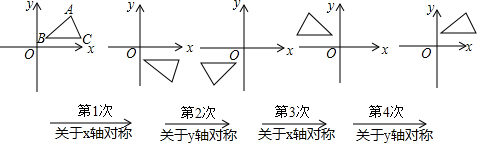
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com