
如图,已知⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,S△ABC=10cm2,C△ABC=10cm,且∠C=60°求:
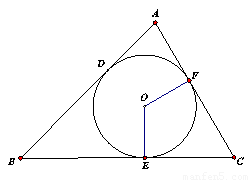
(1)⊙O的半径r;
(2)扇形OEF的面积(结果保留π);
(3)扇形OEF的周长(结果保留π)。
(1)2cm;(2)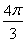 cm2;(3)
cm2;(3)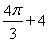 (cm).
(cm).
【解析】
试题分析:(1)连接AO、BO、CO,根据S△ABC=S△AOC+S△AOB+S△BOC即可求出⊙O的半径;
(2)因为OF⊥AC,OE⊥BC,∠C=60°可求出∠EOF的度数,代入扇形面积计算公式即可求出扇形的面积;
(3)利用扇形的周长=扇形的弧长+半径×2,即可求出扇形的周长.
试题解析:(1)如图,连接AO、BO、CO,
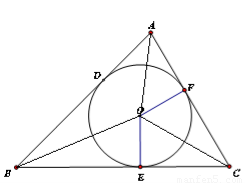
则S△ABC=S△AOC+S△AOB+S△BOC
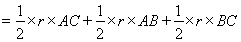
 ,
,
又AB+BC+AC=10,
∴r=2cm;
(2)因为OF⊥AC,OE⊥BC,∠C=60°
所以∠EOF=120°
所以S扇形EOF=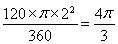 cm2
cm2
(3)扇形EOF的周长=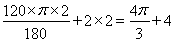 (cm).
(cm).
考点: 1.面积法;2.扇形面积计算;3.扇形弧长计算.


科目:初中数学 来源: 题型:
 23、如图,已知线段AB=8cm,⊙P与⊙Q的半径均为1cm.点P,Q分别从A,B出发,在线段AB上按箭头所示方向运动.当P,Q两点未相遇前,在下列选项中,⊙P与⊙Q不可能出现的位置关系是( )
23、如图,已知线段AB=8cm,⊙P与⊙Q的半径均为1cm.点P,Q分别从A,B出发,在线段AB上按箭头所示方向运动.当P,Q两点未相遇前,在下列选项中,⊙P与⊙Q不可能出现的位置关系是( )查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
求证:(1)CE=DE;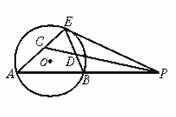
(2)![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com