Question

如图,AB是⊙O的弦,从⊙O上一点C作CD⊥AB于D,作∠OCD的平分线交⊙O于P,M为过P的切线PM上的点,过M作MF⊥OC于F,交PC于E

（1）求证：

（2）请探究ME与MP间的数量关系,并说明理由.

 

Answer 1

【答案】

（1）证明见解析;（2）MP=ME,证明见解析．

【解析】

试题分析：（1）连接OP,得到∠OPC=∠FCP,再由PC平分∠OCD,CD⊥AB,推出OP⊥AB,即可得到结论;

（2）猜想MP=ME,先证明∠EPM=∠MEP,即可得到结论．

试题解析：（1）连接OP,

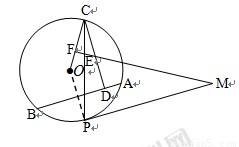
∵OC=OP,

∴∠OPC=∠FCP,

∵PC平分∠OCD,

∴∠OPC=∠FCP=∠PCD,

∴OP//CD,

而CD⊥AB,

∴OP⊥AB,

∴;

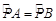（2）MP=ME.

∵PM为⊙O切线,

∴∠OPM=∠OPC+∠EPM=90°,

又∵MF⊥OC,

∴∠OCE+∠CEF=90°,

∴∠OPC+∠EPM=∠OCE+∠CEF=∠OCE+∠MEP,

而∠OCE=∠OPC

∴∠EPM=∠MEP,

∴MP=ME．

考点：垂径定理．