
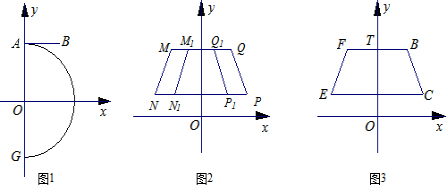
已知:以原点O为圆心,5为半径的半圆与y轴交于A、G两点,AB与半圆相切于点A,点B的坐标为(3, )。(如图1
)。(如图1 )过半圆上的点C
)过半圆上的点C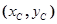 作y轴的垂线,垂足为D.Rt△DOC的面积为
作y轴的垂线,垂足为D.Rt△DOC的面积为 。
。
(1)求点C的坐标;
(2)①命题“如图2,以y轴为对称轴的等腰梯形MNPQ与M1N1P1Q1的上底和下底都分别在同一条直线上,NP∥MQ,PQ∥P1Q1,且NP>MQ.设抛物线y=a0x2+h0过点P、Q,抛物线y=a1x2+h1过点P1、Q1,则h0>h1”是真命题.请你以Q(3,5)、P(4,3)和Q1(p,5)、P1(p+1,3)为例进行验证;
②当图1中的线段BC在第一象限时,作线段BC关于y轴对称的线段FE,连接BF、CE,点T是线段BF上的动点(如图3);设K是过T、B、C三点的抛物线y=ax2+bx+c的顶点,求K的纵坐标yK的取值范围.
(1)C(4,3)(2分)和C(4,-3)
(2)①过点P(4,3)、Q(3,5)的抛物线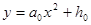
即为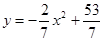 ,得
,得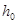 =
=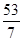 。
。
过P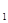 (p+1,3)、Q
(p+1,3)、Q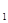 (p,5)的抛物线
(p,5)的抛物线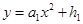
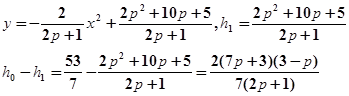
∵MQ>M1Q1,其中MQ=6,可知0≤p<3;∴7p+3>0,2p+1>0,3-p>0,
因而得到h0-h1>0,证得h0>h1.或者说明2p+1>0,-14p2+36p+18在0≤p<3时总是大于0,得到h0-h1>0.
②显然抛物线y=ax2+bx+c的开口方向向下,a<0.
当T运动到B点时,这时B、T、K三点重合即B为抛物线的顶点,∴yK≥5;
将过点T、B、C三点的抛物线y=ax2+bx+c沿x轴平移,使其对称轴为y轴,这时yK不变.
则由上述①的结论,当T在FB上运动时,过F(-3,5)、B(3,5)、C(4,3)三点的抛物线的顶点为最高点,yK≤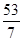 ∴5≤yK≤
∴5≤yK≤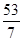
解析


科目:初中数学 来源: 题型:
| 3 | 8 |
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(49):2.8 二次函数的应用(解析版) 题型:解答题
 xC2.
xC2.
查看答案和解析>>
科目:初中数学 来源:第23章《二次函数与反比例函数》中考题集(45):23.5 二次函数的应用(解析版) 题型:解答题
 xC2.
xC2.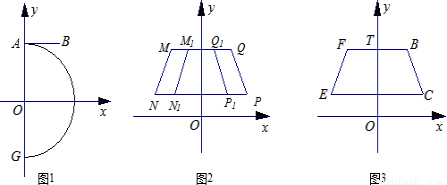
查看答案和解析>>
科目:初中数学 来源:2012年浙江省杭州市西湖区中考数学模拟试卷(七)(解析版) 题型:解答题
 xC2.
xC2.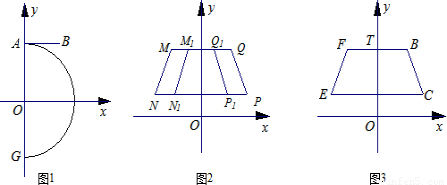
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《二次函数》(06)(解析版) 题型:解答题
 xC2.
xC2.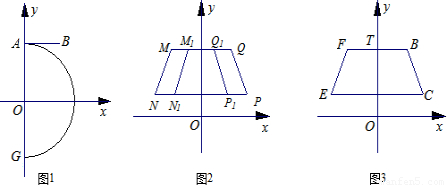
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com