
| 3 |
| 4 |

| 4 |
| x |
| 3 |
| 4 |
| 1 |
| 2 |
| 4 |
| x |

| 1 |
| 2 |
| CF |
| OA |
| CG |
| AB |
| 5 |
| 4 |
| 5 |
| 4 |
| 9 |
| 4 |
| GE |
| AE |
| ||
| 4-m |
| OB |
| OA |
| 3 |
| 4 |
| ||
| 4-m |
| 3 |
| 4 |
| 4 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
| k |
| x |
 意一点,过点P作PC⊥x轴于点C,PO⊥y轴于点D.
意一点,过点P作PC⊥x轴于点C,PO⊥y轴于点D.| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 | 4 |

查看答案和解析>>
科目:初中数学 来源: 题型:
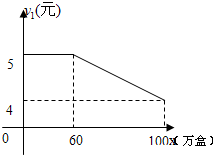 潍坊市昌乐县有一个食品厂,该厂的食品主要有两种销售方式,一种方式是卖给食品经销商,另一种方式是在各超市的柜台进行销售,每年该厂生产的食品都可以全部销售,该食品厂每年可以生产食品100万盒,其中,卖给食品经销商每盒食品的利润y1(元)与销售量x(万盒)之间的函数图如图所示;在各超市柜台销售的每盒利润y2(元)与销售量x(万盒)之间的函数关系为:y2=
潍坊市昌乐县有一个食品厂,该厂的食品主要有两种销售方式,一种方式是卖给食品经销商,另一种方式是在各超市的柜台进行销售,每年该厂生产的食品都可以全部销售,该食品厂每年可以生产食品100万盒,其中,卖给食品经销商每盒食品的利润y1(元)与销售量x(万盒)之间的函数图如图所示;在各超市柜台销售的每盒利润y2(元)与销售量x(万盒)之间的函数关系为:y2=
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 | 4 |
 交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′O′B′.直线A′B′与直线AB相交于点C.
交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′O′B′.直线A′B′与直线AB相交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com