
【题目】如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,
求证:(1)BD平分∠ABC;
(2)△BCD为等腰三角形.

【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)由AB的中垂线MN交AC于点D,交AB于M,求得△ABD是等腰三角形,即可求得∠ABD的度数,然后根据等边对等角,求得∠DBC的度数,从而得证;
(2)根据(1)的结论和外角的性质,可得∠BDC=∠C,再根据等角对等边得证.
试题解析:(1)∵MN为AB的中垂线,
∴AD=BD,
则∠A=∠ABD=36°,
∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∴∠DBC=36°,
因此,BD平分∠ABC;
(2)由①和∠2=36° ∠C=72° ,
∵∠BDC=180°-36°-72°=72°,
∴∠C=∠ABD+∠DBC=∠BDC,
∴△BCD为等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,如果AB∥CD,那么图中相等的内错角是( )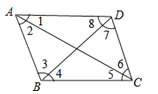
A.∠1与∠5,∠2与∠6
B.∠3与∠7,∠4与∠8
C.∠5与∠1,∠4与∠8
D.∠2与∠6,∠7与∠3
查看答案和解析>>
科目:初中数学 来源: 题型:
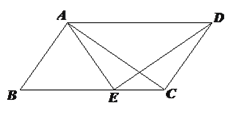
【题目】如图,在四边形ABCD中,AB//CD,∠B=∠ADC,点E是BC边上的一点,且AE=DC.
(1)求证:△ABC≌△EAD ;
(2)如果AB⊥AC,求证:∠BAE= 2∠ACB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明想测量学校教学楼的高度,教学楼AB的后面有一建筑物CD,他测得当光线与地面成22°的夹角时,教学楼在建筑物的墙上留下高2m高的影子CE;而当光线与地面成45°的夹角时,教学楼顶A在地面上的影子F与墙角C有13m的距离(点B,F,C在同一条直线上)
(1)请你帮小明计算一下学校教学楼的高度;
(2)为了迎接上级领导检查,学校准备在AE之间挂一些彩旗,请计算AE之间的长.(结果精确到1m,参考数据:sin22°≈0.375,cos22°≈0.9375,tan22°≈0.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】舌尖上的浪费让人触目惊心,据统计中国每年浪费的食物总量折合粮食约499.5亿千克,这个数用科学记数法应表示为( )
A.4.995×1011B.49.95×1010
C.0.4995×1011D.4.995×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
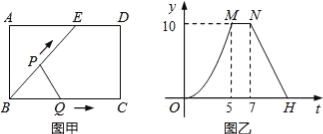
【题目】如图甲,点E为矩形ABCD边AD上一点,点P,Q同时从B点出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为y(![]() ),已知y与t的函数关系的图象如图乙(曲线OM为抛物线的一部分),则下列结论:
),已知y与t的函数关系的图象如图乙(曲线OM为抛物线的一部分),则下列结论:
①当0<t≤5时,y=![]() ;②tan∠ABE=
;②tan∠ABE=![]() ;③点H的坐标为(11,0);④△ABE与△QBP不可能相似.
;③点H的坐标为(11,0);④△ABE与△QBP不可能相似.
其中正确的是 (把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
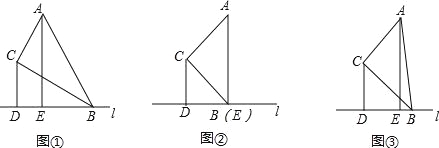
【题目】在△ABC中,∠ACB=90°经过点B的直线l(l不与直线AB重合)与直线BC的夹角等于∠ABC,分别过点C、A做直线l的垂线,垂足分别为点D、E.
(1)问题发现:
①若∠ABC=30°,如图①,则![]() = ;
= ;
②∠ABC=45°,如图②,则![]() = ;
= ;
(2)拓展探究:
当0°<∠ABC<90°,![]() 的值有无变化?请仅就图③的情形给出证明.
的值有无变化?请仅就图③的情形给出证明.
(3)问题解决:
若直线CE、AB交于点F,![]() =
=![]() ,CD=4,请直接写出线段BD的长.
,CD=4,请直接写出线段BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com