
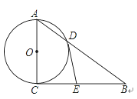
【题目】如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线,与边BC交于点E,若AD=![]() , AC=3.则DE长为( )
, AC=3.则DE长为( )
A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
【答案】B
【解析】
连接OD,CD.由切线长定理得CD=DE,可证明△ADC∽△ACB,则可求得BD,再由勾股定理求得BC,可证明BE=DE,从而求得DE的长.
连接OD,CD.
∵AC为⊙O的直径,
∴∠ADC=90°,
∵AD=![]() ,AC=3.
,AC=3.
∴CD=![]() ,
,
∵OD=OC=OA,
∴∠OCD=∠ODC,
∵DE是切线,
∴∠CDE+∠ODC=90°.
∵∠OCD+∠DCB=90°,
∴∠BCD=∠CDE,
∴DE=CE.
∴△ADC∽△ACB,
∴∠B=∠ACD,
∴![]() ,
,
∴BC=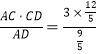 =4,
=4,
∵∠ACD+∠DCB=90°,
∴∠B+∠DCB=90°,∠B+∠CDE=90°,∠CDE+∠BDE=90°,
∴∠B=∠BDE,
∴BE=DE,
∴BE=CE=DE.
∴DE=![]() BC=
BC=![]() ×4=2.
×4=2.
故选:B.


科目:初中数学 来源: 题型:
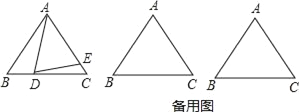
【题目】如图,已知△ABC中,AB=AC=6,BC=8,点D是BC边上的一个动点,点E在AC边上,∠ADE=∠B.设BD的长为x,CE的长为y.
(1)当D为BC的中点时,求CE的长;
(2)求y关于x的函数关系式,并写出x的取值范围;
(3)如果△ADE为等腰三角形,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
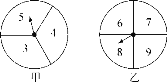
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)该游戏是否公平?如果不公平,请修改游戏规则使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
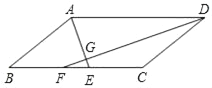
【题目】已知:如图,在ABCD中,∠BAD,∠ADC的平分线AE,DF分别与线段BC相交于点E,F,AE与DF相交于点G.若AD=10,AB=6,AE=4,则DF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行于x轴的直线![]() 分别与一次函数y=-x+3和二次函数y= x2 -2x-3的图象交于A(x1,y1),B(x2,y2),C(x3,y3)三点,且x1<x2<x3,设m= x1+x2+x3,则m的取值范围是____________.
分别与一次函数y=-x+3和二次函数y= x2 -2x-3的图象交于A(x1,y1),B(x2,y2),C(x3,y3)三点,且x1<x2<x3,设m= x1+x2+x3,则m的取值范围是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是抛物线y=﹣x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
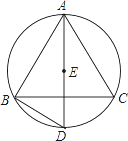
【题目】如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.
(1)当△ABC的外接圆半径为1时,且∠BAC=60°,求弧BC的长度.
(2)连接BD,求证:DE=DB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com