
 过点A′,且它的另一分支与直线l相交于点C,试判断:直线A′C是否经过原点O?
过点A′,且它的另一分支与直线l相交于点C,试判断:直线A′C是否经过原点O?
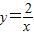 .把y=1代入
.把y=1代入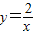 ,得C(2,1),再求得直线AC的解析式为:y=2x,把点O(0,0)代入y=2x,左=右,故直线A'C经过原点O.
,得C(2,1),再求得直线AC的解析式为:y=2x,把点O(0,0)代入y=2x,左=右,故直线A'C经过原点O.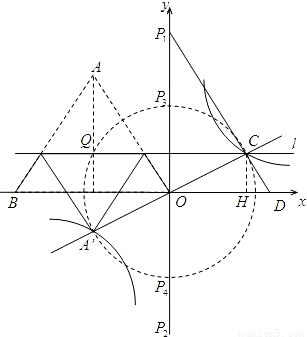
 ,作CH⊥x轴,由△OHC∽△CHD可得:
,作CH⊥x轴,由△OHC∽△CHD可得: ,即CH2=OH•HD,
,即CH2=OH•HD, ,解得:m=-2,故直线CP的解析式为y=-2x+5,令x=0,则y=5.故点P的坐标为P1(0,5).
,解得:m=-2,故直线CP的解析式为y=-2x+5,令x=0,则y=5.故点P的坐标为P1(0,5). ,则点
,则点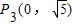 、
、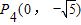 .
.

科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,把等腰△ABO放在直角坐标系中,AB=AO,点A的坐标是(-2,3),过△ABO的重心Q作x轴的平行线l,把△ABO沿直线l翻折,使得点A'落在第三象限.
已知:如图,把等腰△ABO放在直角坐标系中,AB=AO,点A的坐标是(-2,3),过△ABO的重心Q作x轴的平行线l,把△ABO沿直线l翻折,使得点A'落在第三象限.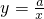 过点A′,且它的另一分支与直线l相交于点C,试判断:直线A′C是否经过原点O?
过点A′,且它的另一分支与直线l相交于点C,试判断:直线A′C是否经过原点O?查看答案和解析>>
科目:初中数学 来源:2012年5月中考数学模拟试卷(40)(解析版) 题型:解答题
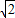 AD.
AD.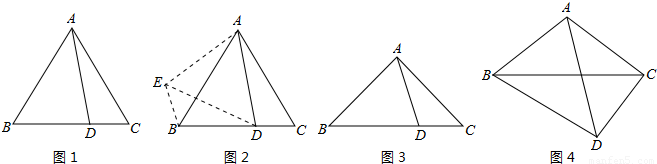
查看答案和解析>>
科目:初中数学 来源:2012年北京市延庆县中考数学一模试卷(解析版) 题型:解答题
 AD.
AD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com