如图，AB为⊙O的直径，点C在⊙O 上，点P是直径AB上的一点，（不与A，B重合），过点P作AB的垂线交BC的延长线于点Q.
（1）点D在线段PQ上，且DQ=DC.
求证：CD是⊙O的切线；
（2）若sinQ=
，BP =6，AP =
，求QC的长.
科目：初中数学 来源： 题型：
如图1，已知抛物线的方程C1：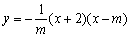
(m＞0)与x轴交于点B、C，与y轴交于点E，且点B在点C的左侧．
（1）若抛物线C1过点M(2, 2)，求实数m的值；
（2）在（1）的条件下，求△BCE的面积；
（3）在（1）的条件下，在抛物线的对称轴上找一点H，使得BH＋EH最小，求出点H的坐标；
（4）在第四象限内，抛物线C1上是否存在点F，使得以点B、C、F为顶点的三角形与△BCE相似？若存在，求m的值；若不存在，请说明理由．
图1
查看答案和解析>>
科目：初中数学 来源： 题型：
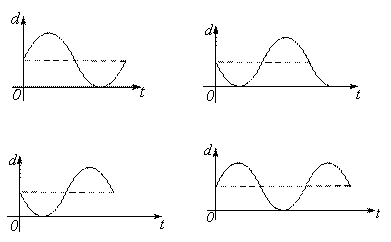
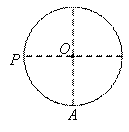
.如右图，⊙O上有两点A与P，且OA⊥OP，若A点固定不动， P点在圆上匀速运动一周， 那么弦AP的长度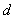
与时间
的函数关系的图象可能是
 |
① ②
③ ④
A. ① B. ③ C. ①或③ D. ②或④
查看答案和解析>>
科目：初中数学 来源： 题型：
定义：把一个半圆与抛物线的一部分合成封闭图形，我们把这个封闭图形称为“蛋圆”．如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线．如图，A，B，C，D分别是“蛋圆”与坐标轴的交点，已知点D的坐标为（0,8），AB为半圆的直径，半圆的圆心M的坐标为（1,0），半圆半径为3．
（1）请你直接写出“蛋圆”抛物线部分的解析式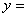
，自变量的取值范围是 ；
（2）请你求出过点C的“蛋圆”切线与x轴的 交点坐标；
（3）求经过点D的“蛋圆”切线的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
有下列四种说法：
(1)由5m＝6m＋2可得m＝2；
(2)方程的解就是方程中未知数所取的值；
(3)方程2x－1＝3的解是x＝2；
(4)方程x＝－x没有解．
其中错误说法的个数是( )．
A．1 
B．2 C．3 D．4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
， 
，
. 
，
.
，∴
.
.
. 
， 
的半径，∴
是⊙
，
中，
， 
，
是⊙
.
中，
.
. 
的图象如图所示，
的值为( )．
C.
D．不能确定
)．