
【题目】如图,在Rt△ABC中,∠A=30°,∠C=90°,E是斜边AB的中点,点P为AC边上一动点,若Rt△ABC的直角边AC=4,则PB+PE的最小值等于_____.

 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】为增强居民节约用水意识,某市在2018年开始对供水范围内的居民用水实行“阶梯收费”,具体收费标准如下表:

某户居民四月份用水10 m3时,缴纳水费23元.
(1) 求a的值;
(2) 若该户居民五月份所缴水费为71元,求该户居民五月份的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴交于点A,B(A在B的左侧),抛物线的对称轴为直线x=1,AB=4. 
(1)求抛物线的表达式;
(2)抛物线上有两点M(x1 , y1)和N(x2 , y2),若x1<1,x2>1,x1+x2>2,试判断y1与y2的大小,并说明理由;
(3)直线l过A及C(0,﹣2),P为抛物线上一点(在x轴上方),过P作PD∥y轴交直线AC于点D,以PD为直径作⊙E,求⊙E在直线AC上截得的线段的最大长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,D是AB边上的一点,过点D作DE∥BC,∠ABC的角平分线于点E.
(1)如图1,当点E恰好在AC边上时,求证:∠ADE=2∠DEB;
(2)如图2,当点D在BA的延长线上时,其余条件不变,请直接写出∠ADE与∠DEB之间的数量关系,并说明理由。
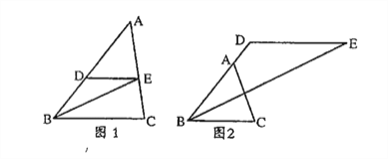
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AD是BC边上的高,∠BDE=∠CDF=30°,在下列结论中:①△ABD≌△ACD;②2DE=2DF=AD;③△ADE≌△ADF;④4BE=4CF=AB.正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AB=6cm,D为边AB中点.动点P、Q在边AB上同时从点D出发,点P沿D→A以1cm/s的速度向终点A运动.点Q沿D→B→D以2cm/s的速度运动,回到点D停止.以PQ为边在AB上方作等边三角形PQN.将△PQN绕QN的中点旋转180°得到△MNQ.设四边形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<3).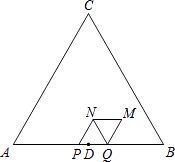
(1)当点N落在边BC上时,求t的值.
(2)当点N到点A、B的距离相等时,求t的值.
(3)当点Q沿D→B运动时,求S与t之间的函数表达式.
(4)设四边形PQMN的边MN、MQ与边BC的交点分别是E、F,直接写出四边形PEMF与四边形PQMN的面积比为2:3时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,点A(0,8),C(6,0).动点P从点B出发,以每秒1个单位长的速度沿射线BC方向匀速运动,设运动时间为t秒.
(1)当t= s时,以OB、OP为邻边的平行四边形是菱形;
(2)当点P在OB的垂直平分线上时,求t的值;
(3)将△OBP沿直线OP翻折,使点B的对应点D恰好落在x轴上,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=4,DE=7,则线段EC的长为( )

A. 3 B. 4 C. 3.5 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人到岛上去探宝,从A处登陆后先往东走4 km,又往北走1.5 km,遇到障碍后又往西走2 km,再折回向北走到4.5 km处往东一拐,仅走0.5 km就找到宝藏.问登陆点A与宝藏埋藏点B之间的距离是多少?
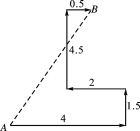
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com