
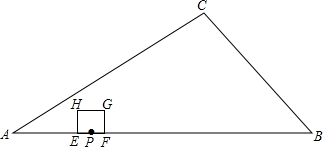
分析 (1)根据题意可以得到当t=1时和t=4时,正方形EFGH的边长;
(2)根据题意可以得到当0<t≤1时和1<t≤3时对应的函数解析,本题得以解决.
解答 解:(1)由题意可得,
当t=1时,PE=1,PF=1,则EF=2,
当x=4时,PE=4-3=2,PF=4,则EF=2+4=6,
故答案为:2,6;
(2)由题意可得,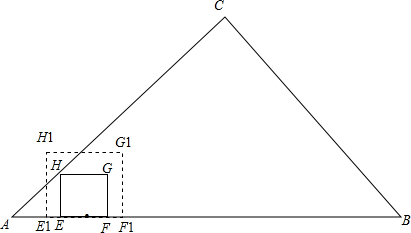 如右图所示,
如右图所示,
∠A=45°,EH=2PE,
当AE=EH时,0<t≤1,2t=3-t,得t=1,S=(2t)2=4t2;
当点E移动到点E1时,1<t≤3,AE1=3-t,则S=$(2t)^{2}-\frac{[2t-(3-t)]^{2}}{2}$=$-\frac{1}{2}{t}^{2}+9t-\frac{9}{2}$;
∴$s=\left\{\begin{array}{l}{4{t}^{2}}&{0<t≤1}\\{-\frac{1}{2}{t}^{2}+9t-\frac{9}{2}}&{1<t≤3}\end{array}\right.$.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
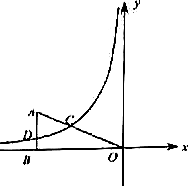 已知:在平面直角坐标系xOy中,过点A(-5,2)向x轴作垂线,垂足为B,连接AO,点C在线段AO上,且AC:CO=2:3,反比例函数y=$\frac{k}{x}$的图象经过点C,与边AB交于点D.
已知:在平面直角坐标系xOy中,过点A(-5,2)向x轴作垂线,垂足为B,连接AO,点C在线段AO上,且AC:CO=2:3,反比例函数y=$\frac{k}{x}$的图象经过点C,与边AB交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l:y=-$\frac{3}{4}$x+b与x轴、y轴分别相交于点A、C,且△AOC的周长为24.
如图,直线l:y=-$\frac{3}{4}$x+b与x轴、y轴分别相交于点A、C,且△AOC的周长为24.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
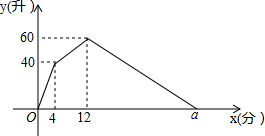 某容器装有两个相同的注水管和一个出水管,注水管的注水速度和出水管的出水速度均为定值,从某一时刻开始,打开两个注水管向容器内注水4分钟,然后关闭一个注水管,打开出水管.出水管出水8分钟,关闭另一个注水管,容器内的水放完时关闭出水管.容器内的水量y(升)与时间x(分)之间的函数图象如图所示.
某容器装有两个相同的注水管和一个出水管,注水管的注水速度和出水管的出水速度均为定值,从某一时刻开始,打开两个注水管向容器内注水4分钟,然后关闭一个注水管,打开出水管.出水管出水8分钟,关闭另一个注水管,容器内的水放完时关闭出水管.容器内的水量y(升)与时间x(分)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
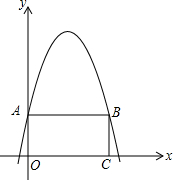 如图,矩形AOCB的两边在坐标轴上,抛物线y=-x2+4x+2经过A、B两点.
如图,矩形AOCB的两边在坐标轴上,抛物线y=-x2+4x+2经过A、B两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com