
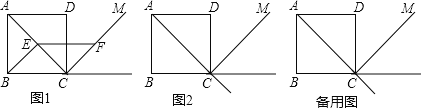
【题目】在正方形ABCD中,点E是射线AC上一点,点F是正方形ABCD外角平分线CM上一点,且CF=AE,连接BE,EF.
(1)如图1,当E是线段AC的中点时,直接写出BE与EF的数量关系;
(2)当点E不是线段AC的中点,其它条件不变时,请你在图2中补全图形,判断(1)中的结论是否成立,并证明你的结论;
(3)当点B,E,F在一条直线上时,求∠CBE的度数.(直接写出结果即可)
【答案】(1)EF=![]() BE;(2)EF=
BE;(2)EF=![]() BE,理由见解析;(3)当B,E,F在一条直线上时,∠CBE=22.5°
BE,理由见解析;(3)当B,E,F在一条直线上时,∠CBE=22.5°
【解析】
(1)证明△ECF是等腰直角三角形即可;
(2)图形如图2所示:(1)中的结论仍然成立,即EF=![]() BE.只要证明BE=DE,△DEF是等腰直角三角形即可;
BE.只要证明BE=DE,△DEF是等腰直角三角形即可;
(3)图形如图2所示:(1)中的结论仍然成立,即EF=![]() BE.只要证明∠CBF=∠CFB即可.
BE.只要证明∠CBF=∠CFB即可.
解:(1)如图1中,结论:EF=![]() BE.
BE.
理由:
∵四边形ABCD是正方形,
∴BA=BC,∠ABC=∠BCD=90°,∠ACD=∠ACB=45°,
∵AE=EC,
∴BE=AE=EC,
∵CM平分∠DCG,
∴∠DCF=45°,
∴∠ECF=90°,
∵CF=AE,
∴EC=CF,
∴EF=![]() EC,
EC,
∴EF=![]() BE.
BE.
(2)图形如图2所示:(1)中的结论仍然成立,即EF=![]() BE.
BE.
理由:连接ED,DF.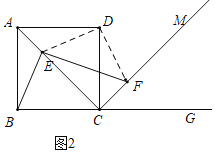
由正方形的对称性可知,BE=DE,∠CBE=∠CDE
∵正方形ABCD,
∴AB=CD,∠BAC=45°,
∵点F是正方形ABCD外角平分线CM上一点,
∴∠DCF=45°,
∴∠BAC=∠DCF,
由∵CF=AE,
∴△ABE≌△CDF(SAS),
∴BE=DF,∠ABE=∠CDF,
∴DE=DF,
又∵∠ABE+∠CBE=90°,
∴∠CDF+∠CDE=90°,
即∠EDF=90°,
∴△EDF是等腰直角三角形
∴EF=![]() DE,
DE,
∴EF=![]() DE.
DE.
(3)如图3中,当点B,E,F在一条直线上时,∠图形如图2所示:(1)中的结论仍然成立,即EF=![]() BE.CBE=22.5°.
BE.CBE=22.5°.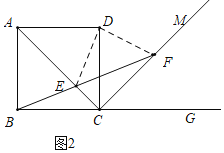
理由:∵∠ECF=∠EDF=90°,
∴E,C,F,D四点共圆,
∴∠BFC=∠CDE,
∵∠ABE=∠ADE,∠ABC=∠ADC=90°,
∴∠CDE=∠CBE,
∴∠CBF=∠CFB,
∵∠FCG=∠CBF+∠CFB=45°,
∴∠CBE=22.5°.


科目:初中数学 来源: 题型:
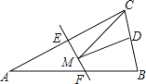
【题目】如图,等腰三角形ABC的底边BC长为4,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,若△CDM周长的最小值为8,则△ABC的面积为( )
A.12B.16C.24D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义一种新的运算“![]() ”:对于任意四个有理数
”:对于任意四个有理数![]() ,
,![]() ,
,![]() ,
,![]() ,可以组成两个有理数对
,可以组成两个有理数对![]() 与
与![]() ,并且规定:
,并且规定:![]() .
.
例如: ![]() .
.
根据上述规定解决下列问题:
(1)计算:![]() ;
;
(2)若有理数对![]() ,则
,则![]() ;
;
(3)若有理数对![]() 成立,则解得
成立,则解得![]() 是整数,求整数
是整数,求整数![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.

调查结果统计表
组别 | 分组 | 人数 |
A |
| 4 |
B |
| 16 |
C |
| a |
D |
| b |
E |
| 2 |
请根据以上图表,解答下列问题:
![]() 填空:这次被调查的同学共有______ 人,
填空:这次被调查的同学共有______ 人, ![]() ______ ,
______ , ![]() ______ ;
______ ;
![]() 求扇形统计图中扇形C的圆心角度数;
求扇形统计图中扇形C的圆心角度数;
![]() 该校共有学生1000人,请估计每月零花钱的数额x在
该校共有学生1000人,请估计每月零花钱的数额x在![]() 范围的人数.
范围的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=30°,以下说法错误的是( )
A. AC=2CDB. AD=2CDC. AD=3BDD. AB=2BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2019年5月30日万州牌楼长江大桥正式通车以来,大放光彩,引万人驻足.市民们纷纷前往打卡、拍照留念,因此牌楼长江大桥成为了万州网红打卡地.周末,小棋和小艺两位同学相约前往参观,小棋骑自行车,小艺步行,她们同时从学校出发,沿同一条路线前往,出发一段时间后小棋发现东西忘了,于是立即以原速返回到学校取,取到东西后又立即以原速追赶小艺并继续前往,到达目的地后等待小艺一起参观(取东西的时间忽略不计),在整个过程两人保持匀速,如图是两人之间的距离![]() 与出发时间
与出发时间![]() 之间的函数图象如图所示,则当小棋到达目的地时,小艺离目的地还有______米.
之间的函数图象如图所示,则当小棋到达目的地时,小艺离目的地还有______米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列单项式:![]() ,
,![]() ,
,![]() ,
,![]() ,…
,…![]() ,
,![]() ,…写出第
,…写出第![]() 个单项式,为了解这个问题,特提供下面的解题思路.
个单项式,为了解这个问题,特提供下面的解题思路.
![]() 这组单项式的系数的符号,绝对值规律是什么?
这组单项式的系数的符号,绝对值规律是什么?
![]() 这组单项式的次数的规律是什么?
这组单项式的次数的规律是什么?
![]() 根据上面的归纳,你可以猜想出第
根据上面的归纳,你可以猜想出第![]() 个单项式是什么?
个单项式是什么?
![]() 请你根据猜想,请写出第
请你根据猜想,请写出第![]() 个,第
个,第![]() 个单项式.
个单项式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,C是⊙O上的一点,连结AC并延长至D,使CD=AC,连结BD,作CE⊥BD,垂足为E.
(1)线段AB与DB的大小关系为___________,请证明你的结论;
(2)求证:CE 是⊙O的切线;
(3)当△CED与四边形ACEB的面积比是1:7时,试判断△ABD的形状,并证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com