
【题目】如图,AB是⊙O的直径,C为AB延长线上一点,过点C作⊙O的切线CD,D为切点,点F是弧AD的中点,连接OF并延长交CD于点E,连接BD,BF.
(1)求证:BD∥OE;
(2)若OE=3![]() ,tanC=
,tanC=![]() ,求⊙O的半径.
,求⊙O的半径.
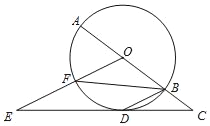
【答案】(1)证明见解析;(2)⊙O的半径的长3![]() .
.
【解析】
(1)如图,由圆的半径相等可得∠1=∠3,再由圆周角定理可得∠1=∠2,从而可得∠2=∠3,继而可得结论;
(2)连接OD,如图,根据切线的性质可得OD⊥CD,根据tanC=![]() ,设OD=3k,CD=4k,继而可得BC=2k,由平行线分线段成比例定理可得
,设OD=3k,CD=4k,继而可得BC=2k,由平行线分线段成比例定理可得 ![]() ,继而可求得DE=6k,在Rt△ODE中,利用勾股定理求出k的值即可得答案.
,继而可求得DE=6k,在Rt△ODE中,利用勾股定理求出k的值即可得答案.
(1)∵OB=OF,
∴∠1=∠3,
∵点F是![]() 的中点,
的中点,
∴∠1=∠2,
∴∠2=∠3,
∴BD∥OE;
(2)连接OD,如图,
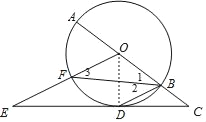
∵直线CD是⊙O的切线,
∴OD⊥CD,
在Rt△OCD中,∵tanC=![]() ,
,
∴设OD=3k,CD=4k.
∴OC=5k,BO=3k,
∴BC=2k.
∵BD∥OE,
∴![]() ,
,
即![]() ,
,
∴DE=6k,
在Rt△ODE中,∵OE2=OD2+DE2,
∴(3![]() )2=(3k)2+(6k)2,
)2=(3k)2+(6k)2,
解得k=![]() ,
,
∴OB=3![]() ,
,
即⊙O的半径的长3![]() .
.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,且∠DAE=90°,连接CE.

(1)如图①,当点D在线段BC上时:
①BC与CE的位置关系为 ;
②BC、CD、CE之间的数量关系为 .
(2)如图②,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若不成立,请你写出正确结论,并给予证明.
(3)如图③,当点D在线段BC的延长线上时,BC、CD、CE之间的数量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(m+1)x2﹣2x﹣1=0有两个不相等的实数根,
(1)求m的取值范围;
(2)若x=1是方程的一个根,求m的值和另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线l:y=![]() x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则
x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则![]() 的长是_____.
的长是_____.
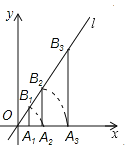
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB 为⊙O 的直径,C 为⊙O 上一点,AD⊥CE 于点 D,AC 平分∠DAB.
(1) 求证:直线 CE 是⊙O 的切线;
(2) 若 AB=10,CD=4,求 BC 的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小李上学用的自行车,型号是24英吋(车轮的直径为24英吋,约60厘米),为了防止在下雨天骑车时的泥水溅到身上,他想在自行车两轮的阴影部分两侧装上挡水的铁皮(两个阴影部分分别是以C、D为圆心的两个扇形),量出四边形ABCD中∠DAB=125°、∠ABC=115°,那么预计需要的铁皮面积约是( )

A. 942平方厘米 B. 1884平方厘米
C. 3768平方厘米 D. 4000平方厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾斜角由45°降为30°,已知原滑滑板AB的长为5米,点D、B、C在同一水平地面上.若滑滑板的正前方能有3米长的空地就能保证安全,原滑滑板的前方有6米长的空地,像这样改造是否可行?请说明理由.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.449)
≈2.449)

查看答案和解析>>
科目:初中数学 来源: 题型:
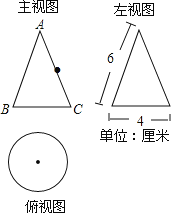
【题目】如图是一个几何体的三视图.
(1)写出该几何体的名称,并根据所示数据计算这个几何体的表面积;
(2)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)阅读理解:
如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′,FD′相交于点O.
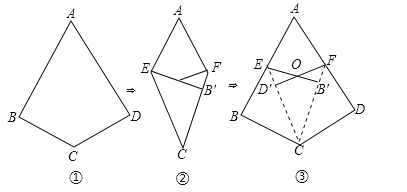
简单应用:
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是 ;
(2)当图③中的∠BCD=120°时,∠AEB′= °;
(3)当图②中的四边形AECF为菱形时,对应图③中的“完美筝形”有 个(包含四边形ABCD).
拓展提升:
(4)当图③中的∠BCD=90°时,连接AB′,请探求∠AB′E的度数,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com