练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．在下列实数中，无理数是（　　）
    A．0B．-$\frac{22}{7}$C．$\sqrt{2}$D．$\sqrt{9}$

    分析 无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．

    解答 解：0，-$\frac{22}{7}$，$\sqrt{9}$是有理数，
    $\sqrt{2}$是无理数，
    故选：C．

    点评 此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    6．对于任意不相等的两个数a，b，定义一种运算*如下：a*b=$\frac{2\sqrt{a+b}}{a-b}$，如3*2=$\frac{2\sqrt{3+2}}{3-2}$=2$\sqrt{5}$，那么12*4的值为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

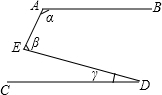    7．如图，AB∥CD，图中α、β、γ三个角之间的数量关系为（　　）
    A．α+β+γ=360°B．α+β-γ=180°C．α+β+γ=180°D．α-β-γ=90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：
    （1）$\sqrt{27}$×$\sqrt{50}$$÷\sqrt{6}$
    （2）2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．对于任意实数x，下列各式中一定成立的是（　　）
    A．$\sqrt{{x}^{2}-1}$=$\sqrt{x-1}$•$\sqrt{x+1}$B．$\sqrt{{（x+1）}^{2}}$=x+1C．$\sqrt{（-4）•（-x）}$=$\sqrt{-4}$•$\sqrt{-x}$D．$\sqrt{3{6x}^{4}}$=6x2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．将一个半径为10cm的圆分成3个扇形，其圆心角的比1：2：3．
    求：（1）各个扇形的圆心角的度数；
        （2）其中最小一个扇形的面积（结果保留π）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，在?ABCD中，∠D=45°，∠CAD=35°，求∠B和∠BAC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．a、b、c为△ABC三边，不是直角三角形的是（　　）
    A．a2=c2-b2B．a=6，b=10，c=8
    C．∠A：∠B：∠C=3：4：5D．a=8k，b=17k，c=15k

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

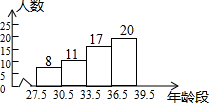    6．菲尔兹奖（Fields Medal）是享有崇高声誉的数学大奖，每四年颁奖一次，颁给二至四名成就显著的年轻数学家，下面是对截至2015年56名获奖者的年龄进行统计得到的统计图．则下列说法中正确的是（　　）
    A．平均年龄是37.5岁B．中位数年龄位于33.5-36.5岁
    C．众数年龄位于36.5-39.5岁D．以上选项都不正确

    查看答案和解析>>

    同步练习册答案