
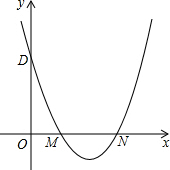
 抛物线y=x2-4x+3交x轴于M,N点(M点在N点左边),交y轴于D点,点E为第一象限抛物线上的点,若∠EMN=2∠ODM,求E点坐标.
抛物线y=x2-4x+3交x轴于M,N点(M点在N点左边),交y轴于D点,点E为第一象限抛物线上的点,若∠EMN=2∠ODM,求E点坐标. 分析 如图取点Q(4,1),作QF⊥x轴于F,QP⊥OD于P,作MQ的垂直平分线交P于K,射线MK与抛物线的交点就是点E的位置,求出直线MK的解析式,通过解方程组可以解决点E坐标.
解答 解:如图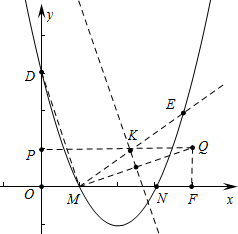 取点Q(4,1),作QF⊥x轴于F,QP⊥OD于P,由题意D(0,3),M(1,0),N(3,0),
取点Q(4,1),作QF⊥x轴于F,QP⊥OD于P,由题意D(0,3),M(1,0),N(3,0),
在△DOM和△MFQ中,
$\left\{\begin{array}{l}{OM=QF}\\{∠DOM=∠MFQ}\\{OD=MF}\end{array}\right.$,
∴△DOM≌△MFQ,
∴∠QMF=∠MOD,
作MQ的垂直平分线交P于K,则KM=KQ,
∴∠KMQ=∠KQM=∠QMF,
∴∠KMF=2∠MDO,射线MK与抛物线的交点就是点E的位置.
∵直线MQ为y=$\frac{1}{3}$x-$\frac{1}{3}$,线段MQ的垂直平分线为y=-3x+8,
∴点K坐标($\frac{5}{2}$,$\frac{1}{2}$),
∵直线MK为y=$\frac{3}{4}$x-$\frac{3}{4}$,
由$\left\{\begin{array}{l}{y=\frac{3}{4}x-\frac{3}{4}}\\{y={x}^{2}-4x+3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{15}{4}}\\{y=\frac{33}{16}}\end{array}\right.$,
∴点E坐标为($\frac{15}{4}$,$\frac{33}{16}$).
点评 本题考查抛物线与x轴的交点、一次函数、全等三角形的判定和性质等知识,解题的关键是找到点E的位置,巧妙利用函数的性质解决交点E坐标,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $2\sqrt{2}-1$ | B. | $2-\sqrt{2}$ | C. | $1-\sqrt{2}$ | D. | $2+\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
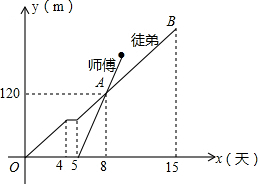 为了检修自来水管道,由师徒两人完成,两人从管道两端开始检修,已知徒弟先修了4天后,休息了1天,接着师徒两人合做了5天,师傅被安排做其他工作,余下由徒弟单独检修完,如图是师傅和徒弟修管道的长度与工作时间的函数图象,请根据图象提供的信心解答下列问题.
为了检修自来水管道,由师徒两人完成,两人从管道两端开始检修,已知徒弟先修了4天后,休息了1天,接着师徒两人合做了5天,师傅被安排做其他工作,余下由徒弟单独检修完,如图是师傅和徒弟修管道的长度与工作时间的函数图象,请根据图象提供的信心解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
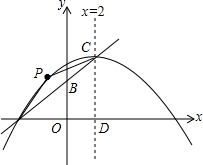 在平面直角坐标系中,A(-4,0),B(0,2),直线x=2与直线AB交于点C,与x轴交于点D,抛物线经过点A,且以C为顶点.
在平面直角坐标系中,A(-4,0),B(0,2),直线x=2与直线AB交于点C,与x轴交于点D,抛物线经过点A,且以C为顶点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点E为正方形ABCD中AD边上的动点,AB=2,以BE为边画正方形BEFG,连结CF和CE,则△CEF面积的最小值为$\frac{3}{2}$.
如图,点E为正方形ABCD中AD边上的动点,AB=2,以BE为边画正方形BEFG,连结CF和CE,则△CEF面积的最小值为$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
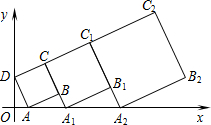 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是5×($\frac{3}{2}$)4030.
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是5×($\frac{3}{2}$)4030.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com