
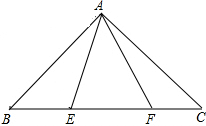
 已知如图,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2.
已知如图,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2.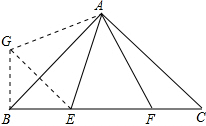 证明:把△ACF绕点A顺时针旋转90°,得到△ABG.连接EG.
证明:把△ACF绕点A顺时针旋转90°,得到△ABG.连接EG.
|


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
| a2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,A、B两个乡镇相距21千米,原计划在两乡镇之间修一条笔直公路以改善交通状况,现在情况有变,为保护环境,县政府决定在以C处为中心方圆10千米的圆形区域内建立绿色生态旅游区,不允许公路从生态区穿过,C处距离A、B两个乡镇分别为20千米和13千米,请通过计算回答,两乡镇间的公路还能按计划实施吗?
如图,A、B两个乡镇相距21千米,原计划在两乡镇之间修一条笔直公路以改善交通状况,现在情况有变,为保护环境,县政府决定在以C处为中心方圆10千米的圆形区域内建立绿色生态旅游区,不允许公路从生态区穿过,C处距离A、B两个乡镇分别为20千米和13千米,请通过计算回答,两乡镇间的公路还能按计划实施吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com