
 如图,AB是⊙O的直径且AB=4$\sqrt{3}$,点C是OA的中点,过点C作CD⊥AB交⊙O于D点,点E是⊙O上一点,连接DE,AE交DC的延长线于点F,则AE•AF的值为12.
如图,AB是⊙O的直径且AB=4$\sqrt{3}$,点C是OA的中点,过点C作CD⊥AB交⊙O于D点,点E是⊙O上一点,连接DE,AE交DC的延长线于点F,则AE•AF的值为12.  课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,直线MN为BC的垂直平分线,交BC于点E,点D在直线MN上,且在△ABC的外面,连接BD,CD,若CA平分∠BCD,∠A=65°,∠ABC=85°,则△BCD是( )
如图,在△ABC中,直线MN为BC的垂直平分线,交BC于点E,点D在直线MN上,且在△ABC的外面,连接BD,CD,若CA平分∠BCD,∠A=65°,∠ABC=85°,则△BCD是( )| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
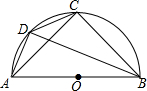 如图,AB是半圆O的直径,点C是$\widehat{AB}$的中点,D是$\widehat{AC}$上一点,且BD-AD=$\sqrt{2}$,则弦CD的长为( )
如图,AB是半圆O的直径,点C是$\widehat{AB}$的中点,D是$\widehat{AC}$上一点,且BD-AD=$\sqrt{2}$,则弦CD的长为( )| A. | $\sqrt{2}$ | B. | $\frac{1}{2}\sqrt{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC是等边三角形,延长BC至D,连接AD,在AD上取一点E,连接BE交AC于F,若AF+CD=AD,DE=2,AF=4,则AD长为7.
如图,△ABC是等边三角形,延长BC至D,连接AD,在AD上取一点E,连接BE交AC于F,若AF+CD=AD,DE=2,AF=4,则AD长为7.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
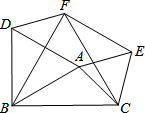 如图,在△ABC中,AB=2,AC=$\sqrt{2}$,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为2.
如图,在△ABC中,AB=2,AC=$\sqrt{2}$,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=8,BC=12,若点P在AD边上,连接BP、PC,△BPC是以PB为腰的等腰三角形,则PB的长为10或12.
如图,在矩形ABCD中,AB=8,BC=12,若点P在AD边上,连接BP、PC,△BPC是以PB为腰的等腰三角形,则PB的长为10或12.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,一条河的两岸有一段是平行的,河宽36米,在河的南岸边每隔几米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边24米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则每两棵树间的间隔5米.
如图所示,一条河的两岸有一段是平行的,河宽36米,在河的南岸边每隔几米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边24米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则每两棵树间的间隔5米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com