
【题目】如图,在等边![]() 中取点
中取点![]() 使得
使得![]() ,
,![]() ,
,![]() 的长分别为3, 4, 5,则
的长分别为3, 4, 5,则![]() _________.
_________.

【答案】![]()
【解析】
把线段AP以点A为旋转中心顺时针旋转60![]() 得到线段AD,由旋转的性质、等边三角形的性质以及全等三角形的判定定理SAS证得△ADB≌△APC,连接PD,根据旋转的性质知△APD是等边三角形,利用勾股定理的逆定理可得△PBD为直角三角形,∠BPD=90
得到线段AD,由旋转的性质、等边三角形的性质以及全等三角形的判定定理SAS证得△ADB≌△APC,连接PD,根据旋转的性质知△APD是等边三角形,利用勾股定理的逆定理可得△PBD为直角三角形,∠BPD=90![]() ,由△ADB≌△APC得S△ADB=S△APC,则有S△APC+S△APB=S△ADB+S△APB=S△ADP+S△BPD,根据等边三角形的面积为边长平方的
,由△ADB≌△APC得S△ADB=S△APC,则有S△APC+S△APB=S△ADB+S△APB=S△ADP+S△BPD,根据等边三角形的面积为边长平方的![]() 倍和直角三角形的面积公式即可得到S△ADP+S△BPD=
倍和直角三角形的面积公式即可得到S△ADP+S△BPD=![]() ×32+
×32+![]() ×3×4=
×3×4=![]() .
.
将线段AP以点A为旋转中心顺时针旋转60![]() 得到线段AD,连接PD
得到线段AD,连接PD
∴AD=AP,∠DAP=60![]() ,
,
又∵△ABC为等边三角形,
∴∠BAC=60![]() ,AB=AC,
,AB=AC,
∴∠DAB+∠BAP=∠PAC+∠BAP,
∴∠DAB=∠PAC,
又AB=AC,AD=AP
∴△ADB≌△APC
∵DA=PA,∠DAP=60![]() ,
,
∴△ADP为等边三角形,
在△PBD中,PB=4,PD=3,BD=PC=5,
∵32+42=52,即PD2+PB2=BD2,
∴△PBD为直角三角形,∠BPD=90![]() ,
,
∵△ADB≌△APC,
∴S△ADB=S△APC,
∴S△APC+S△APB=S△ADB+S△APB=S△ADP+S△BPD=![]() ×32+
×32+![]() ×3×4=
×3×4=![]() .
.
故答案为:![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A',点B、C的对应点分别是点B'、C'.

(1)△ABC的面积是 ;
(2)画出平移后的△A'B'C';
(3)若连接AA'、CC′,这两条线段的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
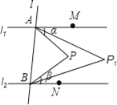
【题目】如图,直线l1∥l2,直线l与l1、l2分别交于A、B两点,点M、N分别在l1、l2上,点M、N、P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.
(1)当点P在l1与l2之间时.
①求∠APB的大小(用含α、β的代数式表示);
②若∠PAM的平分线与∠PBN的平分线交于点P1,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,则∠AP1B= ,∠APnB= .(用含α、β的代数式表示,其中n为正整数)
(2)当点P不在l1与l2之间时.
若∠PAM的平分线与∠PBN的平分线交于点P,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC、BD交于点O,BD⊥AD于点D,将△ABD沿BD翻折得到△EBD,连接EC、EB.
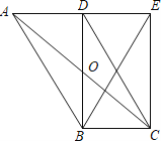
(1)求证:四边形DBCE是矩形;
(2)若BD=4,AD=3,求点O到AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△AEF的顶点E,F分别在BC、CD边上,高AG与正方形的边长相等,连BD分别交AE、AF于点M、N,若EG=4,GF=6,BM= ![]() ,则MN的长为。
,则MN的长为。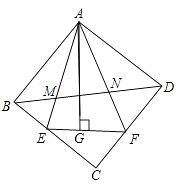
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽想用一块面积为![]() 的正方形纸片,沿着边的方向裁出一块面积为
的正方形纸片,沿着边的方向裁出一块面积为![]() 的长方形纸片,使它的长宽之比为4:3,他不知道能否裁的出来,正在发愁,请你用所学知识帮小丽分析,能否裁出符合要求的纸片.
的长方形纸片,使它的长宽之比为4:3,他不知道能否裁的出来,正在发愁,请你用所学知识帮小丽分析,能否裁出符合要求的纸片.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com