
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ĖıߊĪ![]() ø÷¶„µćµÄ×ų±ź·Ö±šĪŖ
ø÷¶„µćµÄ×ų±ź·Ö±šĪŖ![]() £¬¶Æµć
£¬¶Æµć![]() Óė
Óė![]() Ķ¬Ź±“Ó
Ķ¬Ź±“Ó![]() µć³ö·¢£¬ŌĖ¶ÆŹ±¼äĪŖ
µć³ö·¢£¬ŌĖ¶ÆŹ±¼äĪŖ![]() Ćė£¬µć
Ćė£¬µć![]() ŃŲ
ŃŲ![]() ·½ĻņŅŌ
·½ĻņŅŌ![]() µ„Ī»³¤¶Č/ĆėµÄĖŁ¶ČĻņµć
µ„Ī»³¤¶Č/ĆėµÄĖŁ¶ČĻņµć![]() ŌĖ¶Æ£¬µć
ŌĖ¶Æ£¬µć![]() ŃŲÕŪĻß
ŃŲÕŪĻß![]() ŌĖ¶Æ£¬ŌŚ
ŌĖ¶Æ£¬ŌŚ![]() ÉĻŌĖ¶ÆµÄĖŁ¶Č·Ö±šĪŖ
ÉĻŌĖ¶ÆµÄĖŁ¶Č·Ö±šĪŖ![]() £Øµ„Ī»³¤¶Č/Ćė£©.µ±
£Øµ„Ī»³¤¶Č/Ćė£©.µ±![]() ÖŠµÄŅ»µćµ½“ļ
ÖŠµÄŅ»µćµ½“ļ![]() µćŹ±£¬Į½µćĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ.
µćŹ±£¬Į½µćĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ.
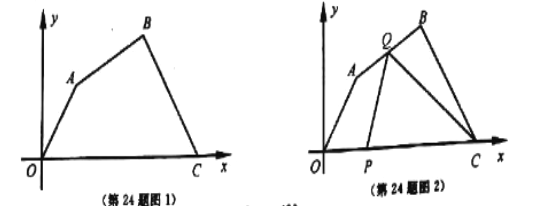
£Ø1£©Ēó![]() ĖłŌŚÖ±ĻßµÄŗÆŹż±ķ“ļŹ½£»
ĖłŌŚÖ±ĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©ČēĶ¼2£¬µ±µć![]() ŌŚ
ŌŚ![]() ÉĻŌĖ¶ÆŹ±£¬Ēó
ÉĻŌĖ¶ÆŹ±£¬Ēó![]() µÄĆ껿
µÄĆ껿![]() ¹ŲÓŚ
¹ŲÓŚ![]() µÄŗÆŹż±ķ“ļŹ½¼°
µÄŗÆŹż±ķ“ļŹ½¼°![]() µÄ×ī“óÖµ£»
µÄ×ī“óÖµ£»
£Ø3£©ŌŚ![]() £¬
£¬![]() µÄŌĖ¶Æ¹ż³ĢÖŠ£¬ČōĻ߶Ī
µÄŌĖ¶Æ¹ż³ĢÖŠ£¬ČōĻ߶Ī![]() µÄ“¹Ö±Ę½·ÖĻß¾¹żĖıߊĪ
µÄ“¹Ö±Ę½·ÖĻß¾¹żĖıߊĪ![]() µÄ¶„µć£¬ĒóĻąÓ¦µÄ
µÄ¶„µć£¬ĒóĻąÓ¦µÄ![]() Öµ.
Öµ.
”¾“š°ø”æ(1) y=![]() x+2
x+2![]() ;(2)
;(2) ![]() ,µ±t=5Ź±£¬SÓŠ×ī“óÖµ£»×ī“óÖµĪŖ
,µ±t=5Ź±£¬SÓŠ×ī“óÖµ£»×ī“óÖµĪŖ![]() ;(3) tµÄÖµĪŖ
;(3) tµÄÖµĪŖ![]() .
.
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©ÓĆ“ż¶ØĻµŹż·ØĒóÖ±ĻßABµÄ½āĪöŹ½¼“æÉ£»£Ø2£©øł¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½µĆµ½¹ŲÓŚtµÄ¶ž“ĪČżĻīŹ½£¬ŌŁÓɶž“ĪŗÆŹżĶ¼ĻńµÄŠŌÖŹĒó³öSµÄ×ī“óÖµ¼“æÉ£»£Ø3£©øł¾ŻtµÄÖµ·ÖĒéæöĢÖĀŪ£¬ŅĄĢāŅāĮŠ³ö²»Ķ¬µÄ·½³Ģ“Ó¶ųĒó³ötµÄÖµ.
ŹŌĢā½āĪö£ŗ
£Ø1£©½ā£ŗ°ŃA£Ø3£¬3 £©£¬B£Ø9£¬5 £©“śČėy=kx+b,
µĆ  ;
;
½āµĆ£ŗ ;
;
”ąy=![]() x+2
x+2![]() ;
;
£Ø2£©½ā£ŗŌŚ”÷PQCÖŠ£¬PC=14-t,PC±ßÉĻµÄøßĻß³¤ĪŖ![]() ;
;
”ą![]()
”ąµ±t=5Ź±£¬SÓŠ×ī“óÖµ£»×ī“óÖµĪŖ![]() .
.
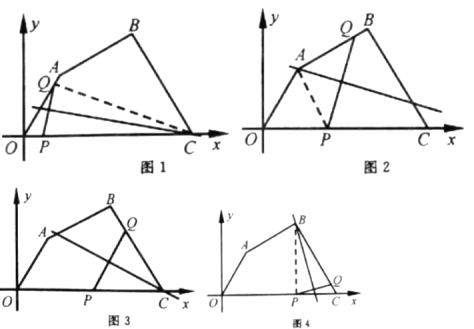
£Ø3£©½ā£ŗ a.µ±0£¼t”Ü2Ź±£¬Ļ߶ĪPQµÄÖŠ“¹Ļß¾¹żµćC£ØČēĶ¼1£©£»
æɵƷ½³Ģ![]()
½āµĆ£ŗ![]() £ØÉįČ„£©£¬“ĖŹ±t=
£ØÉįČ„£©£¬“ĖŹ±t=![]() .
.
b.µ±2£¼t”Ü6Ź±£¬Ļ߶ĪPQµÄÖŠ“¹Ļß¾¹żµćA£ØČēĶ¼2£©
æɵƷ½³Ģ![]() ,
,
½āµĆ£ŗ![]() £ØÉįČ„£©£¬“ĖŹ±
£ØÉįČ„£©£¬“ĖŹ±![]() £»
£»
c.µ±6£¼t”Ü10Ź±£¬
¢ŁĻ߶ĪPQµÄÖŠ“¹Ļß¾¹żµćC£ØČēĶ¼3£©
æɵƷ½³Ģ14-t=25-![]() ;
;
½āµĆ£ŗt=![]() .
.
¢ŚĻ߶ĪPQµÄÖŠ“¹Ļß¾¹żµćB£ØČēĶ¼4£©
æɵƷ½³Ģ![]() ;
;
½āµĆ![]() £ØÉįČ„£©£»
£ØÉįČ„£©£»
“ĖŹ±![]() £»
£»
×ŪÉĻĖłŹö£ŗtµÄÖµĪŖ![]() .
.


 ѧĮ·æģ³µµĄæŚĖćŠÄĖćĖŁĖćĢģĢģĮ·ĻµĮŠ“š°ø
ѧĮ·æģ³µµĄæŚĖćŠÄĖćĖŁĖćĢģĢģĮ·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»Į¾Āż³µ“Ó¼×µŲŌČĖŁŠŠŹ»ÖĮŅŅµŲ£¬Ņ»Į¾æģ³µĶ¬Ź±“ÓŅŅµŲ³ö·¢ŌČĖŁŠŠŹ»ÖĮ¼×µŲ£¬Į½³µÖ®¼äµÄ¾ąĄė![]() £ØĒ§Ć×£©ÓėŠŠŹ»Ź±¼ä
£ØĒ§Ć×£©ÓėŠŠŹ»Ź±¼ä![]() £ØŠ”Ź±£©µÄ¶ŌÓ¦¹ŲĻµČēĶ¼ĖłŹ¾£ŗ
£ØŠ”Ź±£©µÄ¶ŌÓ¦¹ŲĻµČēĶ¼ĖłŹ¾£ŗ

£Ø1£©¼×ŅŅĮ½µŲĻą¾ą¶ąŌ¶£æ
£Ø2£©Ēóæģ³µŗĶĀż³µµÄĖŁ¶Č·Ö±šŹĒ¶ąÉŁ£æ
£Ø3£©Ēó³öĮ½³µĻąÓöŗó![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£Ø4£©ŗĪŹ±Į½³µĻą¾ą![]() Ē§Ć×.
Ē§Ć×.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪOABC·ÅŌŚŅŌOĪŖŌµćµÄĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬A£Ø3£¬0£©£¬C£Ø0£¬2£©£¬µćEŹĒABµÄÖŠµć£¬µćFŌŚBC±ßÉĻ£¬ĒŅCF=1£®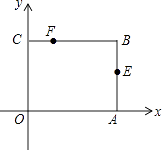
£Ø1£©µćEµÄ×ų±źĪŖ £¬ µćFµÄ×ų±źĪŖ£»
£Ø2£©µćE¹ŲÓŚxÖįµÄ¶Ō³ĘµćĪŖE”䣬µćF¹ŲÓŚyÖįµÄ¶Ō³ĘµćĪŖF”䣬
¢ŁµćE”äµÄ×ų±źĪŖ £¬ µćF”äµÄ×ų±źĪŖ£»
¢ŚĒóÖ±ĻßE”äF”äµÄ½āĪöŹ½£»
£Ø3£©ČōMĪŖxÖįÉĻµÄ¶Æµć£¬NĪŖyÖįÉĻµÄ¶Æµć£¬µ±ĖıߊĪMNFEµÄÖܳ¤×īŠ”Ź±£¬Ēó³öµćM£¬NµÄ×ų±ź£¬²¢Ēó³öÖܳ¤µÄ×īŠ”Öµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČōijÉĢĘ·µÄŌ¼ŪĪŖ100ŌŖ£¬Į¬ŠųĮ½“ĪÕĒ¼ŪŗóµÄŹŪ¼ŪĪŖ144ŌŖ£¬ÉčĮ½“ĪĘ½Ōö³¤ĀŹĪŖx£®ŌņĻĀĆęĖłĮŠ·½³ĢÕżČ·µÄŹĒ£Ø £©
A.100£Ø1©x£©2=144
B.100£Ø1+x£©2=144
C.100£Ø1©2x£©2=144
D.100£Ø1©x£©2=144
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚÄ³“ĪŹŌŃéÖŠ£¬²āµĆĮ½øö±äĮæmŗĶvÖ®¼äµÄ4×é¶ŌÓ¦Źż¾ŻČēĻĀ±ķ£ŗ
m | 1 | 2 | 3 | 4 |
v | 0.01 | 2.9 | 8.03 | 15.1 |
ŌņmÓėvÖ®¼äµÄ¹ŲĻµ×ī½Ó½üÓŚĻĀĮŠø÷¹ŲĻµŹ½ÖŠµÄ( )
A. v£½2m£1B. v£½m2£1C. v£½3m£3D. v£½m£«1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ×ŪŗĻĢā
£Ø1£©øŠÖŖ£ŗČēĶ¼¢Ł£¬ĖıߊĪABCD”¢CEFG¾łĪŖÕż·½ŠĪ£®Ņ×ÖŖBE=DG£®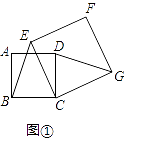
£Ø2£©Ģ½¾æ£ŗČēĶ¼¢Ś£¬ĖıߊĪABCD”¢CEFG¾łĪŖĮāŠĪ£¬ĒŅ”ĻA=”ĻF£®ĒóÖ¤£ŗBE=DG£®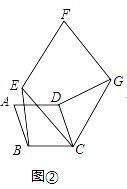
£Ø3£©ČēĶ¼¢Ū£¬ĖıߊĪABCD”¢CEFG¾łĪŖĮāŠĪ£¬µćEŌŚ±ßADÉĻ£¬µćGŌŚADµÄŃÓ³¤ĻßÉĻ£®ČōAE=3ED£¬”ĻA=”ĻF£¬”÷EBCµÄĆ껿ĪŖ8£¬ŌņĮāŠĪCEFGµÄĆ껿ĪŖ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
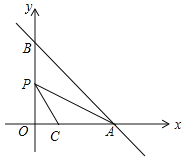
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Ö±Ļßy=©x+m·Ö±š½»xÖį£¬yÖįÓŚA£¬BĮ½µć£¬ŅŃÖŖµćC£Ø2£¬0£©£®
£Ø1£©µ±Ö±ĻßAB¾¹żµćCŹ±£¬µćOµ½Ö±ĻßABµÄ¾ąĄėŹĒ £»
£Ø2£©ÉčµćPĪŖĻ߶ĪOBµÄÖŠµć£¬Į¬½įPA£¬PC£¬Čō”ĻCPA=”ĻABO£¬ŌņmµÄÖµŹĒ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚ”÷ABCÖŠ£¬”ĻA=30”ć£¬µćP“ÓµćA³ö·¢ŅŌ2cm/sµÄĖŁ¶ČŃŲÕŪĻßA©C©BŌĖ¶Æ£¬µćQ“ÓµćA³ö·¢ŅŌa£Øcm/s£©µÄĖŁ¶ČŃŲABŌĖ¶Æ£¬P£¬QĮ½µćĶ¬Ź±³ö·¢£¬µ±Ä³Ņ»µćŌĖ¶Æµ½µćBŹ±£¬Į½µćĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ£®ÉčŌĖ¶ÆŹ±¼äĪŖx£Øs£©£¬”÷APQµÄĆ껿ĪŖy£Øcm2£©£¬y¹ŲÓŚxµÄŗÆŹżĶ¼ĻóÓÉC1£¬C2Į½¶Ī×é³É£¬ČēĶ¼2ĖłŹ¾£®
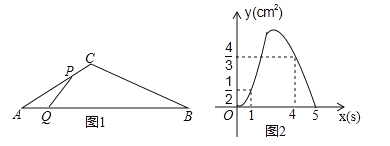
£Ø1£©ĒóaµÄÖµ£»
£Ø2£©ĒóĶ¼2ÖŠĶ¼ĻóC2¶ĪµÄŗÆŹż±ķ“ļŹ½£»
£Ø3£©µ±µćPŌĖ¶Æµ½Ļ߶ĪBCÉĻijŅ»¶ĪŹ±”÷APQµÄĆ껿£¬“óÓŚµ±µćPŌŚĻ߶ĪACÉĻČĪŅāŅ»µćŹ±”÷APQµÄĆ껿£¬ĒóxµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖ¹ÄĄų½ŚŌ¼ÓĆĖ®£¬Ä³ŹŠ×ŌĄ“Ė®¹«Ė¾¶Ō¾ÓĆńÓĆĖ®²ÉÓĆŅŌ»§ĪŖµ„Ī»·Ö¶Ī¼Ę·Ń°ģ·ØŹÕ·Ń£¬¼“Ņ»øöŌĀÓĆĖ®10tŅŌÄŚ£Ø°üŗ¬10t£©µÄÓĆ»§£¬ŹÕĖ®·ŃaŌŖ/t£¬Ņ»ŌĀÓĆĖ®³¬¹ż10tµÄÓĆ»§£¬³¬³öµÄ²æ·Ö°“bŌŖ/t£Øb£¾a£©ŹÕ·Ń£¬ÉčŅ»»§¾ÓĆńÓĆĖ®x t£¬Ó¦ŹÕĖ®·ŃyŌŖ£¬yÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½ČēĶ¼ĖłŹ¾£ŗ°“ÉĻŹö·Ö¶ĪŹÕ·Ń±ź×¼£¬Š”Ą¼¼Ņ3ŌĀ·ŻŗĶ4ŌĀ·Ż·Ö±š½»Ė®·Ń29.1ŌŖŗĶ20.8ŌŖ£¬ŌņŠ”Ą¼¼Ņ4ŌĀ·Ż±Č3ŌĀ·Ż½ŚŌ¼ÓĆĖ®¶Ö£®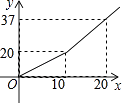
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com