
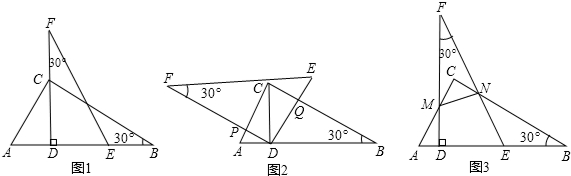
分析 (1)首先判断出∠BCD=∠CAD=60°,然后根据∠ADP+∠PDC=90°,∠CDQ+∠PDC=90°,判断出∠CDQ=∠ADP,根据三角形相似的判定方法,即可判断出△CQD∽△APD.
(2)首先求出AD=3,CD=3$\sqrt{3}$,然后根据△CQD∽△APD,判断出$\frac{CQ}{AP}=\frac{CD}{AD}$,推得CQ=$\sqrt{3}$x,最后根据三角形的面积公式,求出S△PCQ关于x的函数关系式即可.
(3)△MCN面积存在最大值.首先设AM=x,分别求出CM、CN的长度各是多少;然后根据S△MCN=$\frac{1}{2}MC•CN$,求出S△MCN关于x的函数关系式;最后应用配方法,求出△MCN的面积的最大值是多少即可.
解答 (1)证明:∵DF过点C,DF⊥AB,
∴CD⊥AB,
∴∠CDB=∠CDA=90°,∠BCD=90°-30°=60°,
∵∠ACB=90°,
∴∠CAD=90°-30°=60°,
∴∠BCD=∠CAD,
即∠DCQ=∠DAP,
∵∠ADP+∠PDC=90°,∠CDQ+∠PDC=90°,
∴∠CDQ=∠ADP,
在△CQD和△APD中,
$\left\{\begin{array}{l}{∠DCQ=∠DAP}\\{∠CDQ=∠ADP}\end{array}\right.$
∴△CQD∽△APD.
(2)解:如图2,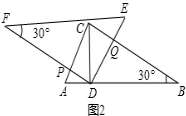 ,
,
∵在Rt△ADC中,AC=6,∠CAD=60°,∠ACD=30°,
∴AD=3,CD=3$\sqrt{3}$,
∵△CQD∽△APD,
∴$\frac{CQ}{AP}=\frac{CD}{AD}$=$\frac{3\sqrt{3}}{3}=\sqrt{3}$,
∴CQ=$\sqrt{3}AP$=$\sqrt{3}$x,
∴S△PCQ=$\frac{1}{2}CQ•CP$=$\frac{\sqrt{3}}{2}x$(6-x)=-$\frac{\sqrt{3}}{2}$x2$+3\sqrt{3}$x(0<x<6).
(3)解:△MCN面积存在最大值.
如图3,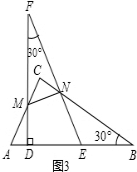 ,
,
∵∠DEF=60°,∠DEF=∠ENB+∠EBN,
∴∠ENB=∠DEF-∠EBN=60°-30°=30°,
∴∠ENB=∠EBN=30°,
∴△BEN是等腰三角形,
设AM=x,则CM=6-x,AD=$\frac{1}{2}$x,
∴BE=AB-AD-DE=12-$\frac{1}{2}x$-6=6-$\frac{1}{2}$x,BN=$\sqrt{3}$(6-$\frac{1}{2}$x),
∴CN=BC-BN=6$\sqrt{3}$-$\sqrt{3}$(6-$\frac{1}{2}x$)=$\frac{\sqrt{3}}{2}$x,
∴S△MCN=$\frac{1}{2}$(6-x)×$\frac{\sqrt{3}}{2}$x=$\frac{\sqrt{3}}{4}$[9-(x-3)2],
∴当x=3时,S△MCN 的最大值为$\frac{9}{4}\sqrt{3}$.
点评 (1)此题主要考查了相似形综合题,考查了三角形相似的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.
(2)此题还考查了三角形的面积的求法,以及二次函数的最值的求法,要熟练掌握.


科目:初中数学 来源: 题型:选择题
| A. | x=2是不等式2x>4的解 | B. | 方程2x=3x没有解 | ||
| C. | 二元一次方程x+y=2有无数组解 | D. | x<0是不等式2x<1的解集 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
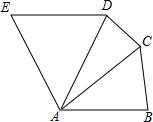 如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )
如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )| A. | 150° | B. | 160° | C. | 130° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
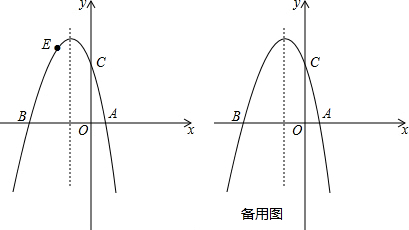
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
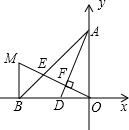 如图,A(0,4),B(-4,0),D(-2,0),OE⊥AD于F,交AB于E,BM⊥OB交OE的延长线于M.
如图,A(0,4),B(-4,0),D(-2,0),OE⊥AD于F,交AB于E,BM⊥OB交OE的延长线于M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com