

分析 (1)根据折叠的性质可得∠ADB=∠EDB,再根据两直线平行,内错角相等可得∠ADB=∠DBC,然后求出∠FBD=∠FDB,根据等角对等边可得BF=DF,设BF=x,表示出CF,在Rt△CDF中,利用勾股定理列出方程求解即可;
(2)根据MN∥PQ,MQ∥AP,所以四边形MNPQ是平行四边形,过点N分别做NE⊥MQ,NF⊥QP,垂足分别为E、F,可得NF=NE,根据S平行四边形MNPQ=NE•MQ=NF•PQ,所以MQ=PQ,所以四边形MNPQ是菱形.
解答 解:(1)由折叠得,∠ADB=∠EDB,
∵矩形ABCD的对边AD∥BC,
∴∠ADB=∠DBC,
∴∠FBD=∠FDB,
∴BF=DF,
设BF=x,则CF=8-x,
在Rt△CDF中,CD2+CF2=DF2
即32+(8-x)2=x2,
解得:x=$\frac{73}{16}$,
即BF=$\frac{73}{16}$;
(2)四边形MNPQ的形状是菱形,
证明:∵矩形纸片ABCD和A′B′C′D′,
∴MN∥PQ,MQ∥AP,
∴四边形MNPQ是平行四边形,①
如图2,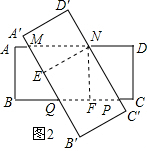
过点N分别做NE⊥MQ,NF⊥QP,垂足分别为E、F,
∴NF=NE,
∵S平行四边形MNPQ=NE•MQ=NF•PQ,
∴MQ=PQ,②
由①②知,四边形MNPQ是菱形.
点评 本题考查了翻折变换的性质,矩形的性质,勾股定理的应用,菱形的判定与性质,熟记翻折的性质并利用勾股定理列出方程是解题的关键.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:初中数学 来源: 题型:填空题
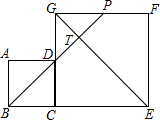 如图,边长分别为3和5的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则ET的长为4$\sqrt{2}$.
如图,边长分别为3和5的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则ET的长为4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
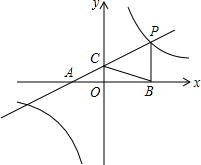 如图,点P是直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$在第一象限内的一个交点,直线y=$\frac{1}{2}$x+2与x轴、y轴的交点分别为A、C,过P作PB垂直于x轴,若AB+PB=9,则△PBC的面积为( )
如图,点P是直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$在第一象限内的一个交点,直线y=$\frac{1}{2}$x+2与x轴、y轴的交点分别为A、C,过P作PB垂直于x轴,若AB+PB=9,则△PBC的面积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$的图象的两个交点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
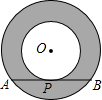 如图,半径均为整数的同心圆组成的“圆环带”,若大圆的弦AB与小圆相切于点P,且弦AB的长度为定值$4\sqrt{3}$,则满足条件的不全等的“圆环带”有( )
如图,半径均为整数的同心圆组成的“圆环带”,若大圆的弦AB与小圆相切于点P,且弦AB的长度为定值$4\sqrt{3}$,则满足条件的不全等的“圆环带”有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无数个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com