
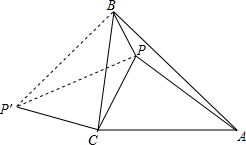
 如图,△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,且AP=3,CP=2,BP=1,求∠BPC得度数.(提示:把△CAP绕点C逆时针旋转90°到△CBP′,证明△BPP′为Rt△)
如图,△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,且AP=3,CP=2,BP=1,求∠BPC得度数.(提示:把△CAP绕点C逆时针旋转90°到△CBP′,证明△BPP′为Rt△) 分析 首先把△CAP绕点C逆时针旋转90°到△CBP′,可得△CPP′是等腰直角三角形,继而求得PP′的长,然后由勾股定理的逆定理可得△BPP′是直角三角形,继而求得答案.
解答 解:把△CAP绕点C逆时针旋转90°到△CBP′,
则∠PCP′=∠ACB=90°,PC=P′C,BP′=AP=3,
∴∠CPP′=45°,PP′=$\sqrt{2}$CP=2$\sqrt{2}$,
在△BPP′中,BP2=12=1,BP′2=32=9,PP′2=(2$\sqrt{2}$)2=8,
∴BP2+BP′2=PP′2,
∴∠BPP′=90°,
∴∠BPC=∠CPP′+∠BPP′=135°.
点评 此题考查了旋转的性质、等腰直角三角形的性质以及勾股定理的逆定理.注意准确作出辅助线是解此题的关键.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交$\widehat{BC}$于D.
如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交$\widehat{BC}$于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,电线杆上有盏路灯O,小明从点F出发,沿直线FM运动,当他运动2米到达点D处时,测得影长DN=0.6m,再前进2米到达点B处时,测得影长MB=1.6m,(图中线段AB、CD、EF表示小明的身高)
如图,电线杆上有盏路灯O,小明从点F出发,沿直线FM运动,当他运动2米到达点D处时,测得影长DN=0.6m,再前进2米到达点B处时,测得影长MB=1.6m,(图中线段AB、CD、EF表示小明的身高)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com