
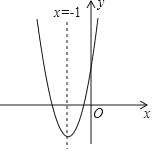
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:
①b2=4ac;②abc>0;③a>c; ④4a﹣2b+c>0,其中正确有_____(填序号).
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() ,已知四边形
,已知四边形![]() 是矩形,且
是矩形,且![]() (0,6),
(0,6),![]() (8,0),若反比例函数
(8,0),若反比例函数![]() 的图象经过线段
的图象经过线段![]() 的中点
的中点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .设直线
.设直线![]() 的解析式为
的解析式为![]() .
.

(1)求反比例函数和直线![]() 的解析式;
的解析式;
(2)求![]() 的面积:
的面积:
(3)请直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2015次运动后,动点P的坐标是( )

A. (2015,0) B. (2015,1) C.(2015,2) D.(2016,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1为全体奇数排成的数表,用十字框任意框出5个数,记框内中间这个数为 a(如图2).
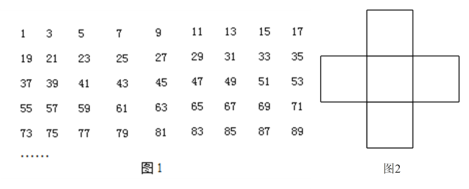
(1)请用含a的代数式表示框内的其余4个数;
(2)框内的5个数之和能等于 2015,2020 吗?若不能,请说明理由;若能,请求出这5个数中最小的一个数,并写出最小的这个数在图1数表中的位置.(自上往下第几行,自左往右的第几个)
查看答案和解析>>
科目:初中数学 来源: 题型:
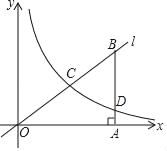
【题目】如图,在平面直角坐标系中,O为坐标原点,经过原点的直线l与反比例函数![]() (x>0)的图象交于点C,B是直线l上的点,过点B作BA⊥x轴,垂足为点A,且C是OB中点,已知OA=4,BD=3.
(x>0)的图象交于点C,B是直线l上的点,过点B作BA⊥x轴,垂足为点A,且C是OB中点,已知OA=4,BD=3.
(1)用含k的代数式来表示D点的坐标为_____;
(2)求反比例函数的解析式;
(3)连接CD,求四边形OADC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为传播优秀数学文化,展现数学的内涵和魅力,提高学生的数学兴趣和素养,江苏教育出版社《时代学习报》与江苏省教育学会中学数学教学专业委员会共同举办初中数学文化节、初三数学应用与创新邀请赛,分别设有一、二、三等奖和纪念奖.某校参加此项比赛,获奖情况已汇制成如图所示的两幅不完整的统计图,根据图中所示信息解答下列问题:
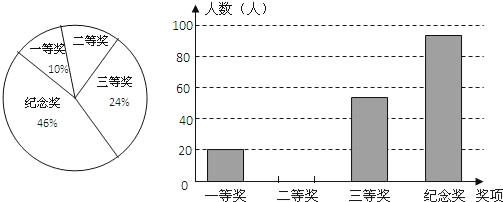
(1)该校一共有 名学生获奖;
(2)这次数学竞赛获二等奖人数是多少?
(3)请将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
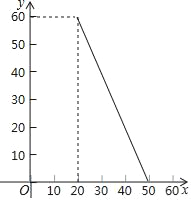
【题目】某商店经销一种小家电,每个小家电的成本为20元,市场调查发现,该种小家电每天的销售量y(个)与销售单价x(元)的函数图象如图.设这种小家电每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)如果物价部门规定这种小家电的销售单价不高于32元,该商店销售这种小家电每天要获得400元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
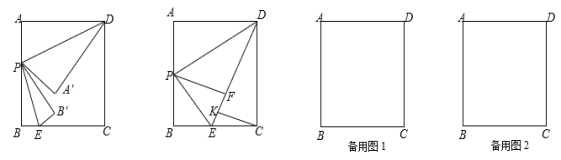
【题目】如图,在矩形ABCD中,AB=8,BC=6,点P、点E分别是边AB、BC上的动点,连结DP、PE.将△ADP与△BPE分别沿DP与PE折叠,点A与点B分别落在点A′,B′处.
(1) 当点P运动到边AB的中点处时,点A′与点B′重合于点F处,过点C作CK⊥EF于K,求CK的长;
(2) 当点P运动到某一时刻,若P,A',B'三点恰好在同一直线上,且A'B'=4 ,试求此时AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农科所甲、乙试验田各有水稻3万个,为了考察水稻穗长的情况,于同一天在这两块试验田里分别随机抽取了![]() 个稻穗进行测量,获得了它们的长度
个稻穗进行测量,获得了它们的长度![]() (单位:cm),并对数据(穗长)进行了整理、描述和分析.下面给出了部分信息.
(单位:cm),并对数据(穗长)进行了整理、描述和分析.下面给出了部分信息.
a.甲试验田穗长的频数分布统计表如下表所示(不完整):
甲试验田穗长频数分布表
分组/ | 频数 | 频率 |
| 4 | 0.08 |
| 9 | 0.18 |
|
| |
| 11 | 0.22 |
|
| 0.20 |
| 2 | |
合计 | 50 | 1.00 |
b.乙试验田穗长的频数分布直方图如图所示:
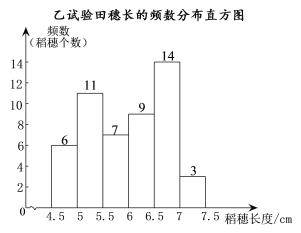
c.乙试验田穗长在![]() 这一组的是:
这一组的是:
6.3 6.4 6.3 6.3 6.2 6.2 6.1 6.2 6.4
d.甲、乙试验田穗长的平均数、中位数、众数、方差如下(表2):
试验田 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 5.924 | 5.8 | 5.8 | 0.454 |
乙 | 5.924 |
| 6.5 | 0.608 |
根据以上信息,回答下列问题:
(1)表中![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
(2)表中![]() 的值为 ;
的值为 ;
(3)在此次考察中,稻穗生长(长度)较稳定的试验田是 ;
A.甲 B.乙 C.无法推断
(4)若穗长在![]() 范围内的稻穗为“良好”,请估计甲试验田所有“良好”的水稻约为 万个.
范围内的稻穗为“良好”,请估计甲试验田所有“良好”的水稻约为 万个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com