
【题目】如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向。为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行多少小时即可到达? (结果保留根号)

【答案】渔船立刻加速以75海里/小时的速度继续航行![]() 小时即可到达.
小时即可到达.
【解析】
如图,过点P作PQ⊥AB交AB延长线于点Q,过点M作MN⊥AB交AB延长线于点N,通过解直角△AQP、直角△BPQ求得PQ的长度,即MN的长度,然后通过解直角△BMN求得BM的长度,则易得所需时间.
如图,过点P作PQ⊥AB交AB延长线于点Q,过点M作MN⊥AB交AB延长线于点N,
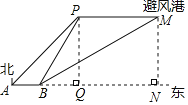
在直角△AQP中,∠PAQ=45°,则AQ=PQ=60×1.5+BQ=90+BQ(海里),
所以 BQ=PQ-90.
在直角△BPQ中,∠BPQ=30°,则BQ=PQtan30°=![]() PQ(海里),
PQ(海里),
所以 PQ-90=![]() PQ,
PQ,
所以 PQ=45(3+![]() )(海里)
)(海里)
所以 MN=PQ=45(3+![]() )(海里)
)(海里)
在直角△BMN中,∠MBN=30°,
所以 BM=2MN=90(3+![]() )(海里)
)(海里)
所以![]() (小时)
(小时)
即渔船立刻加速以75海里/小时的速度继续航行![]() 小时即可到达.
小时即可到达.
故答案是:![]() .
.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】直线y=2x+3与抛物线y=ax2交于A、B两点,已知点A的横坐标为3.
(1)求A、B两点的坐标及抛物线的解析式;
(2)O为坐标原点,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AD//BC,∠BCD=90,对角线AC、BD相交于点E,且AC⊥BD.
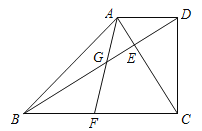
(1)求证:![]() ;
;
(2)点F是边BC上一点,联结AF,与BD相交于点G.如果∠BAF =∠DBF,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=90°,AB=7,AD=2,BC=3,如果边AB上的点P使得以P,A,D为顶点的三角形和以P,B,C为顶点的三角形相似,则这样的P点共有几个( )
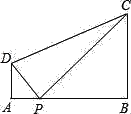
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
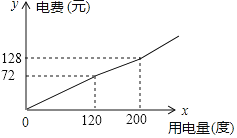
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD的值最小时,点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD的值最小时,点P的坐标为( )

A.(﹣1,0)B.(﹣2,0)C.(﹣3,0)D.(﹣4,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是正方形,点E是边BC上的任意一点,AE⊥EF,且直线EF交正方形外角的平分线CF于点F.
(1)如图1,求证:AE=EF;
(2)如图2,当AB=2,点E是边BC的中点时,请直接写出FC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆高铁与一辆动车组列车在长为1320千米的京沪高速铁路上运行,已知高铁列车比动车组列车平均速度每小时快99千米,且高铁列车比动车组列车全程运行时间少3小时,求这辆高铁列车全程运行的时间和平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
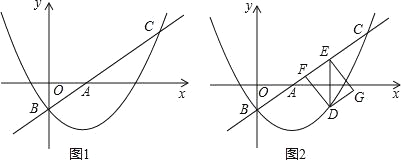
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com