
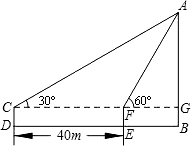
 ���꡶��ֱ�������Ρ����º�һ����ѧ����ʱ����ѧ��ȤС����Ž������Һ�����������У�������ͼ��ʾ�Ľ�ѧ¥�ĸ߶�AB��
���꡶��ֱ�������Ρ����º�һ����ѧ����ʱ����ѧ��ȤС����Ž������Һ�����������У�������ͼ��ʾ�Ľ�ѧ¥�ĸ߶�AB������ ��Rt��AFG�У�����������Ǻ����Ķ���ó�FG=$\frac{AG}{tan��AFG}$=$\frac{AG}{\sqrt{3}}$��ͬ���ɵó�CG=$\frac{AG}{tan��ACG}$=$\sqrt{3}$AG������CG-FG=40���AG�ij��������ɵó����ۣ�
��� �⣺��Rt��AFG�У�
��tan��AFG=$\frac{AG}{FG}$��
��FG=$\frac{AG}{tan��AFG}$=$\frac{AG}{\sqrt{3}}$��
��Rt��ACG��tan��ACG=$\frac{AG}{CG}$��
��CG=$\frac{AG}{tan��ACG}$=$\sqrt{3}$AG��
�֡�CG-FG=40����$\sqrt{3}$AG-$\frac{AG}{\sqrt{3}}$=40��
��AG=20$\sqrt{3}$��
��AB=20$\sqrt{3}$+1.5���ף���
���ⴱ��ѧ¥�ĸ߶�ABΪ��20$\sqrt{3}$+1.5���ף�
���� ���⿼����ǽ�ֱ�������ε�Ӧ��-���Ǹ������⣬���������Ǻ����Ķ����ǽ�����Ĺؼ���


 һ����������ϵ�д�
һ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��$\frac{1}{3}$ | B�� | 2��-$\frac{1}{3}$ | C�� | 3��$\frac{1}{2}$ | D�� | 2��-$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5��x+1��=5.7 | B�� | 5.7��x-1��=5 | C�� | 5��x+1��2=5.7 | D�� | 5+5x=5.7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��6+x=7��x=7+6 | B�� | ��3x+2=5x��3x-5x=2 | ||
| C�� | ��2x=3��x=$\frac{2}{3}$ | D�� | ��2x+4=2��x+2=1 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com