
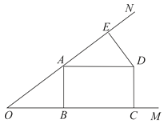
【题目】如图,点A在∠MON的边ON上,AB⊥OM于B,AE=OB,DE⊥ON于E,AD=AO,DC⊥OM于C.
(1)求证:四边形ABCD是矩形;
(2)若DE=3,OE=9,求AB、AD的长.
【答案】(1)证明见解析;(2)AB、AD的长分别为3和5.
【解析】
(1)证Rt△ABO≌Rt△DEA(HL)得∠AOB=∠DAE,AD∥BC.证四边形ABCD是平行四边形,又![]() ,故四边形ABCD是矩形;(2)由(1)知Rt△ABO≌Rt△DEA,AB=DE=3.设AD=x,则OA=x,AE=OE-OA=9-x.在Rt△DEA中,由
,故四边形ABCD是矩形;(2)由(1)知Rt△ABO≌Rt△DEA,AB=DE=3.设AD=x,则OA=x,AE=OE-OA=9-x.在Rt△DEA中,由![]() 得:
得:![]() .
.
(1)证明:∵AB⊥OM于B,DE⊥ON于E,
∴![]() .
.
在Rt△ABO与Rt△DEA中,
∵![]() ∴Rt△ABO≌Rt△DEA(HL).
∴Rt△ABO≌Rt△DEA(HL).
∴∠AOB=∠DAE.∴AD∥BC.
又∵AB⊥OM,DC⊥OM,∴AB∥DC.
∴四边形ABCD是平行四边形.
∵![]() ,∴四边形ABCD是矩形;
,∴四边形ABCD是矩形;
(2)由(1)知Rt△ABO≌Rt△DEA,∴AB=DE=3.
设AD=x,则OA=x,AE=OE-OA=9-x.
在Rt△DEA中,由![]() 得:
得:
![]() ,解得
,解得![]() .
.
∴AD=5.即AB、AD的长分别为3和5.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于⊙O,A是弧BDC的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且弧BF=弧AD.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元,设小明快递物品x千克.
(1)根据题意,填写下表:
快递物品重量(千克) | 0.5 | 1 | 3 | 4 | … |
甲公司收费(元) | 22 | … | |||
乙公司收费(元) | 11 | 51 | 67 | … |
(2)设甲快递公司收费y1元,乙快递公司收费y2元,分别写出y1,y2关于x的函数关系式;
(3)当x>3时,小明应选择哪家快递公司更省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
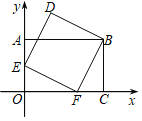
【题目】如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为( )
A. (1,2.5)B. (1,1+ ![]() )C. (1,3)D. (
)C. (1,3)D. (![]() ﹣1,1+
﹣1,1+ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )

A. AB∥DC,AD=BC B. AB∥DC,AD∥BC C. AB=DC,AD=BC D. OA=OC,OB=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M,交BE于点G,AD平分∠MAC,交BC于点D,交BE于点F.
(1)判断直线BE与线段AD之间的关系,并说明理由;
(2)若∠C=30°,图中是否存在等边三角形?若存在,请写出来并证明;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:

(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com