
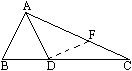
如图所示,已知AD是∠ABC的角平分线,且∠B=2∠C
求证:AC=AB+BD
|
证明:在AC上截取AF=AB,连DF. 在△ABD和△AFD中 所以 △ABD≌△AFD, 所以 BD=DF, ∠B=∠AFD. 又因为 ∠B=2∠C, ∠AFD=∠C+∠FDC, 所以 ∠C=∠FDC, DF=CF. 所以 BD=CF. 所以 AC=AF+FC=AB+BD. 分析:要证AC=AB+BD,由于没有提供这样结论的图形特征,故想到把它们变成证明线段相等的问题:由于AD是角平分,是“对称轴”为此在AC上截取AF=AB,将△ABD翻折到△ADF的位置,只需证BD=CF. 点拨:形如a+b=c的问题叫和差问题,解决此类问题,经常采用的方法是: (1)截取法:若c>a,根据图形适当作出f=c-a,然后证f=b. (2)延长法:根据图形适当作出d=a+b,然后证d=c,或适当作出a+e=c,然后证e=b. 此类问题常与轴对称图形相关,所作出的和线段或差线段一般构成轴对称图形.如此题的△ADF与△ADB是轴对称图形. |


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
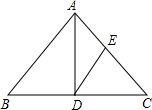 如图所示,已知AD是等腰△ABC底边上的高,且tan∠B=
如图所示,已知AD是等腰△ABC底边上的高,且tan∠B=| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com