
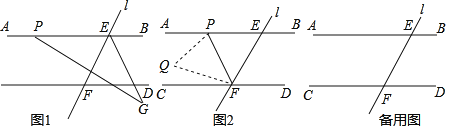
【题目】如图1,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点)
(1)若∠CFE=119°,PG交∠FEB的平分线EG于点G,∠APG=150°,则∠G的大小为 .
(2)如图2,连接PF.将△EPF折叠,顶点E落在点Q处.
①若∠PEF=48°,点Q刚好落在其中的一条平行线上,请直接写出∠EFP的大小为 .
②若∠PEF=75°,∠CFQ=![]() ∠PFC,求∠EFP的度数.
∠PFC,求∠EFP的度数.
【答案】(1)29.5°;(2)①42°或66°;②35°或63°.
【解析】
(1)根据平行线的性质和三角形的内角和即可得到结论;
(2)①Ⅰ、当点Q落在AB上时,利用三角形内角和定理计算即可.Ⅱ、当点Q落在CD上时,∠PQF=∠PEF=48°,利用平行线的性质,三角形的内角和定理计算即可.
②分两种情形:Ⅰ、当点Q在平行线AB,CD之间时.Ⅱ、当点Q在CD下方时,分别构建方程即可解决问题.
(1)∵直线AB∥CD,
∴∠BEF=∠CFE=119°,∠PEF=180°﹣∠CFE=61°,
∵EG平分∠BEF,
∴∠FEG=![]() ∠BEF=59.5°,
∠BEF=59.5°,
∵∠APG=150°,
∴∠EPF=30°,
∴∠G=180°﹣30°﹣61°﹣59.5°=29.5°;
故答案为:29.5°;
(2)①Ⅰ、当点Q落在AB上时,

易证PF⊥AB,可得∠EPF=90°,
∴∠EFP=90°﹣∠PEF=90°﹣48°=42°.
Ⅱ、当点Q落在CD上时,∠PQF=∠PEF=48°,
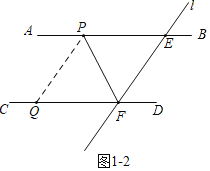
∵AB∥CD,
∴∠EPQ+∠PQF=180°,
∴∠EPQ=132°,
∵∠EPF=∠QPF,
∴∠EPF=![]() ×132°=66°,
×132°=66°,
∴∠EFP=180°﹣48°﹣66°=66°.
综上所述,满足条件的∠EFP的值为42°或66°,
故答案为:42°或66°.
②Ⅰ、当点Q在平行线AB,CD之间时.
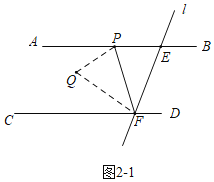
设∠PFQ=x,由折叠可知∠EFP=x,
∵2∠CFQ=∠CFP,
∴∠PFQ=∠CFQ=x,
∴75°+3x=180°,
∴x=35°,
∴∠EFP=35°.
Ⅱ、当点Q在CD下方时,
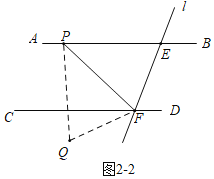
设∠PFQ=x,由折叠可知∠EFP=x,
∵2∠CFQ=∠CFP,
∴∠PFC=![]() x,
x,
∴75°+![]() x+x=180°,
x+x=180°,
解得x=63°,
∴∠EFP=63°.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】探究下面的问题:
(1)如图甲,在边长为a的正方形中去掉一个边长为b的小正方形(a>b),把余下的部分剪拼成如图乙的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是________(用式子表示),即乘法公式中的___________公式.
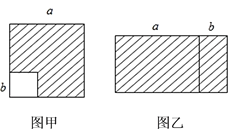
(2)运用你所得到的公式计算:
①10.7×9.3
②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 上一点,且
上一点,且![]() ,连接
,连接![]() 并延长
并延长![]() 交
交![]() 于
于![]() ,又过
,又过![]() 作
作![]() 的垂线交
的垂线交![]() 于
于![]() ,交
,交![]() 为
为![]() ,则下列说法:①
,则下列说法:①![]() 是
是![]() 的中点;②
的中点;②![]() ;③
;③![]() ;④
;④![]() 为等腰三角形;⑤连接
为等腰三角形;⑤连接![]() ,若
,若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为24;其中正确的是______(填序号).
的面积为24;其中正确的是______(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a≠0)的图象如图所示,对称轴是x=-1.下列结论:①ab>0;②b2>4ac;③a-b+2c<0;④8a+c<0.其中正确的是( )

A. ③④ B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A(0,4),交x轴于点B.
(1)求直线AB的表达式和点B的坐标;
(2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.
①用含n的代数式表示△ABP的面积;
②当S△ABP=8时,求点P的坐标;
③在②的条件下,以PB为斜边在第一象限作等腰直角△PBC,求点C的坐标.
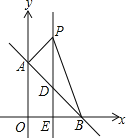
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,∠ACB=90°,AC=BC=4,D是AB的中点,P是平面上的一点,且DP=1,连接BP,CP
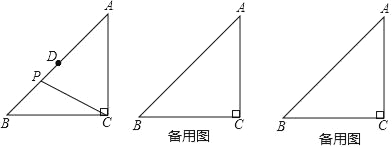
(1)如图,当点P在线段BD上时,求CP的长;
(2)当△BPC是等腰三角形时,求CP的长;
(3)将点B绕点P顺时针旋转90°得到点B′,连接AB′,求AB′的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=2,C是弧AB的中点,AE,BE分别平分∠BAC和∠ABC,以E为圆心,AE为半径作扇形EAB,π取3,则阴影部分的面积为( )

A. ![]() ﹣4 B. 7
﹣4 B. 7![]() ﹣4 C. 6﹣
﹣4 C. 6﹣![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com