D
分析:先根据题意画出图形,再利用正多边形内角和定理求出每个内角的度数,在A
1A
5连接线上取一点P.使A
1P=a.连接A
1A
3、A
3A
5、A
2P,再分别根据等腰三角形及等边三角形的性质解答.
解答:
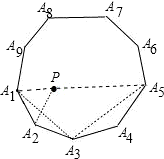
解:如图所示正九边形的内角为140°.
在A
1A
5连接线上取一点P.使A
1P=a.
连接A
1A
3,
∵△A
2A
1A
3是等腰三角形,而∠A
1A
2A
3=140°.
∴∠A
2A
1A
3=20°.
连接A
3A
5,△A
1A
3A
5也是等腰三角形.
而∠A
1A
3A
5=140°-20°-20°=100°.
连接A
2P,
∴∠A
3A
1A
5=40°.
∴∠A
2A
1A
5=60°,可知△A
1A
2P是正三角形.
∴∠A
1PA
2=60°.
△A
2A
3P是等腰三角形.而∠A
3A
2P=140°-60°=80°,
∴∠A
2A
3P=∠A
2PA
3=50°,
∠A
5A
3P=140°-50°-20°=70°,∠A
5PA
3=180°-60°-50°=70°,
∴△A
3A
5P是等腰三角形,而A
5P=A
3A
5=A
1A
3=b,
∴A
1A
5=A
1P+PA
5=a+b.
故选D.
点评:本题考查的是正多边形和圆,根据题意画出图形,作出辅助线是解答此题的关键.


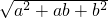
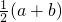
 解:如图所示正九边形的内角为140°.
解:如图所示正九边形的内角为140°.

 名校课堂系列答案
名校课堂系列答案