
����Ŀ���Ķ�������
��A��B�������Ϸֱ��ʾʵ��![]() ��
��![]() ��A��B����֮��ľ������AB. ��A��B��������һ��Ϊԭ��ʱ��������A����ԭ�㡣����ͼ����ʾ����AB =OB =
��A��B����֮��ľ������AB. ��A��B��������һ��Ϊԭ��ʱ��������A����ԭ�㡣����ͼ����ʾ����AB =OB =![]() ��
��![]() .
.
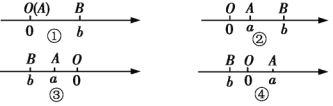
��A��B���㶼����ԭ��ʱ��
��1����ͼ����ʾ����A��B����ԭ����ұߣ��������A�ڵ�B����࣬��AB��OB��OA��![]() ��
��![]() ��
��![]() ��
��![]()
��2����ͼ����ʾ����A��B����ԭ�����ߣ��������A�ڵ�B���Ҳ࣬��AB��OB��OA��![]() ��
��![]() ��
��![]() ��
��![]()
��3������ͼ����ʾ����A��B�ֱ���ԭ������ߣ��������A�ڵ�O���Ҳ࣬��AB��OB��OA��![]() ��
��![]() ��
��![]()
�ش��������⣺
������������������A��B����֮��ľ���AB���������� ����.
�������ϱ�ʾ2��![]() ������A��B֮��ľ���AB�������� ������.
������A��B֮��ľ���AB�������� ������.
�������ϱ�ʾx��![]() ������A��B֮��ľ���AB������ �� �������AB��2����x��ֵΪ������ ��.
������A��B֮��ľ���AB������ �� �������AB��2����x��ֵΪ������ ��.
��������ʽ![]() ����Сֵ������СֵΪ .
����Сֵ������СֵΪ .

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
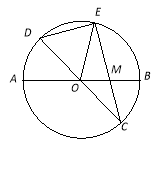
����Ŀ����֪����ͼ���ڰ뾶Ϊ4����O�У�AB��CD������ֱ����MΪOB���е㣬CM���ӳ��߽���O�ڵ�E����EM��MC������DE��DE��![]() ��
��
��1����֤��![]() ��
��
��2����EM�ij���
��3����sin��EOB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У��Ե�AΪԲ�ģ������ⳤΪ�뾶��Բ�����ֱ�AD��AB�ڵ�M��N���ٷֱ��Ե�M��NΪԲ�ģ��Դ���![]() ��Ϊ�뾶��Բ�����������ڵ�P��������AP����CD�ڵ�E������E��EF��AD��AB�ڵ�F����AB=5��CE=2�����ı���ADEF���ܳ�Ϊ______��
��Ϊ�뾶��Բ�����������ڵ�P��������AP����CD�ڵ�E������E��EF��AD��AB�ڵ�F����AB=5��CE=2�����ı���ADEF���ܳ�Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��a��0���ĶԳ���Ϊֱ��x=1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��a��0���ĶԳ���Ϊֱ��x=1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��4ac��b2��
������![]() ����������x1=��1��x2=3��
����������x1=��1��x2=3��
��3a+c��0
����y��0ʱ��x��ȡֵ��Χ�ǩ�1��x��3
����x��0ʱ��y��x���������
���н�����ȷ�ĸ����ǣ�������

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һλС�����ڴֲڲ��ġ�Z������ƽ�����Ϲ���һ���뾶Ϊ10cm��Բ�̣���ͼ��ʾ��AB��CD��ˮƽ�ģ�BC��ˮƽ��ļн�Ϊ60�㣬����AB=60cm��CD=40cm��BC=40cm����ô��С���ѽ�Բ�̴�A�������D����Բ����������·�߳�Ϊ___________cm

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����AB��CD�������BPD���B����D�Ĺ�ϵ��˵�����ɣ�
�⣺�����BPD+��B+��D=360��
���ɣ�����P��EF��AB��
���B+��BPE=180�㣨��ֱ��ƽ�У�ͬ���ڽǻ�����
��AB��CD��EF��AB��
��EF��CD�����������ֱ�߶��͵�����ֱ��ƽ�У���ô������ֱ��Ҳ����ƽ�У���
���EPD+��D=180�㣨��ֱ��ƽ�У�ͬ���ڽǻ�����
���B+��BPE+��EPD+��D=360��
���B+��BPD+��D=360��
��1����������Ľ��ⷽ�����۲�ͼ��2������֪AB��CD������ͼ�еġ�BPD���B����D�Ĺ�ϵ����˵�����ɣ�
��2���۲�ͼ��3���ͣ�4������֪AB��CD������ͼ�еġ�BPD���B����D�Ĺ�ϵ������Ҫ˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��3�£�ij�н������ܲ����ڳ������п�չ������������֪ʶ���������������������ȡ�˲���ͬѧ�ijɼ���x��Ϊ�������ܷ�100�֣��������������в�������ͳ��ͼ����
������ͳ�Ʊ�
��� | ���ɼ����飨��λ���֣� | ��Ƶ�� | ��Ƶ�� |
��A | ��80��x��85 | ��50 | ��0.1 |
��B | ��85��x��90 | ��75 | |
��C | ��90��x��95 | ��150 | ��c |
��D | ��95��x��100 | ��a | |
���ϼ� | ��b | 1 |
����������Ϣ����������⣺
��1��ͳ�Ʊ��У�a=_____��b=_____��c=_____��
��2������ͳ��ͼ�У�m��ֵΪ_____����C������Ӧ��Բ�ĽǵĶ�����_____��
��3�����μӱ��ξ�����ͬѧ����5000�ˣ�������Ƴɼ���95�ּ����ϵ�ѧ����Լ�ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ6��������![]() �Ƶ�
�Ƶ�![]() ��˳ʱ�뷽����ת
��˳ʱ�뷽����ת![]() ��õ�������
��õ�������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ____________��
____________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCO�ı�OA��OC���������ϣ���B����Ϊ��6��6������������ABCO�Ƶ�C��ʱ����ת�ǶȦ���0�㣼����90�㣩���õ�������CDEF��ED���߶�AB�ڵ�G��ED���ӳ��߽��߶�OA�ڵ�H����CH��CG��

��1����֤����CBG�ա�CDG��
��2������HCG�Ķ��������ж��߶�HG��OH��BG֮���������ϵ��˵�����ɣ�
��3������BD��DA��AE��EB�õ��ı���AEBD������ת�����У��ı���AEBD�ܷ�Ϊ���Σ�����ܣ��������H�����ꣻ������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com