Question

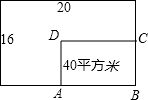
某单位为了响应政府发出的“全民健身”的号召，打算在长和宽分别为20米和16米的矩形大厅内修建一个40平方米的矩形健身房ABCD，该健身房的四面墙壁中有两面沿用大厅的旧墙壁（如图为平面示意图），且每面旧墙壁上所沿用的旧墙壁长度不得超过其长度的一半，己知装修旧墙壁的费用为20元/平方米，新建（含装修）墙壁的费用为80元/平方米，设健身房高3米，健身房AB的长为x米，BC的长为y米，修建健身房墙壁的总投资为w元．
（1）求y与x的函数关系式，并写出自变量x的范围．
（2）求w与x的函数关系，并求出当所建健身房AB长为8米时总投资为多少元？

Answer 1

解：（1）根据题意可知，
∵
∴5≤x≤10

（2）根据题可知w=（x+）×3×80+（x+）×3×20=300×（x+），
当x=8时，（元）．
分析：（1）解析式相对简单，自变量取值范围只需根据“所沿用的旧墙壁长度不得超过其长度的一半”即可求出．
（2）总投资有两部分构成，旧墙和新建墙，应该根据（1）中结果，把这两部分用含x的式子分别表示出来，即可求解．
点评：此题主要考查反比例函数在实际生活中的应用，解题关键是把实际问题转化为数学问题，抽象到反比例函数中．