
已知二次函数y=ax2+bx+c(a>0)的图象与x轴交于A(x1,0)、B(x2,0)(x1<x2)两点,与y轴交于点C,x1,x2是方程x2 +4x﹣5=0的两根.
+4x﹣5=0的两根.
(1)若抛物线的顶点为D,求S△ABC:S△ACD的值;
(2)若∠ADC=90°,求二次函数的解析式.
(1)解方 程x2+4x﹣5=0,得x=﹣5或x=1,
程x2+4x﹣5=0,得x=﹣5或x=1,
由于x1<x2,则有x1=﹣5,x2=1,∴A(﹣5,0),B(1,0).
抛物线的解析式为:y=a(x+5)(x﹣1)(a>0),
∴对称轴为直线x=2,顶点D的坐标为(﹣2,﹣9a),
令x=0,得y=﹣5a,
∴C点的坐标为(0,﹣5a).
依题意画出图形,如右图所示,则OA=5,OB=1,AB=6,OC=5a,
过点D作DE⊥y轴于点E,则DE=2,OE=9a,CE=OE﹣OC=4a.
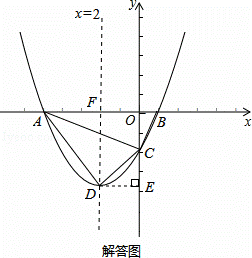 S△ACD=S梯形ADEO﹣S△CDE﹣S△AOC
S△ACD=S梯形ADEO﹣S△CDE﹣S△AOC
=(DE+OA)•OE﹣DE•CE﹣OA•OC
=(2+5)•9a﹣×2×4a﹣×5×5a
=15a,
而S△ABC=AB•OC=×6×5a=15a,
∴S△ABC:S△ACD=15a:15a=1; ……3分
(2)如解答图所示,
在Rt△DCE中,由勾股定理得:CD2=DE2+CE2=4+16a2,
在Rt△AOC中,由勾股定理得:AC2=OA2+OC2=25+25a2,
设对称轴x=2与x轴交于点F,则AF=3,
在Rt△ADF中,由勾股定理得:AD2=AF2+DF2=9+81a2.
∵∠ADC=90°,∴△ACD为直角三角形,
由勾股定理得:AD2+CD2=AC2,
即(9+81a2)+(4+16a2)=25+25a2,化简得:a2=,
∵a>0,
∴a=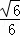 ,
,
∴抛物线的解析式为:y=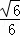 (x+5)(x﹣1)=
(x+5)(x﹣1)=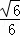 x2+
x2+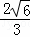 x﹣
x﹣ .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
在矩形ABCD中,AB = 10,BC = 12,E为DC的中点,
连接BE,作AF⊥BE,垂足为F.
(1)求证:△BEC∽△ABF;
(2)求AF的长.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
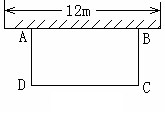
如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,
其中一边AB靠墙,墙长为12m,设AD的长为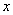 m,DC的长为
m,DC的长为 m.
m.
(1)求 与
与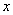 之间的函数关系式;
之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和
DC的长都是整米数,求出满足条件的所有围建方案.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
一只不透明的袋子中装有2个白球和一个红球,这些球除颜色外其余都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,请用树状图或列表的方法列出所有可能的结果,求出两次摸出的球颜色相同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com