
【题目】一次函数![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() .顶点为
.顶点为![]() 的抛物线经过点
的抛物线经过点![]() .
.
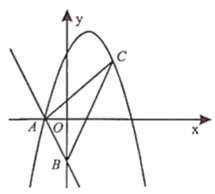
(1)求抛物线的解析式;
(2)点![]() 为第一象限抛物线上一动点.设点
为第一象限抛物线上一动点.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() .当
.当![]() 为何值时,
为何值时,![]() 的值最大,并求
的值最大,并求![]() 的最大值;
的最大值;
(3)在(2)的结论下,若点![]() 在
在![]() 轴上,
轴上,![]() 为直角三角形,请直接写出点
为直角三角形,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 的值最大,最大值为
的值最大,最大值为![]() ;(3)
;(3)![]() 、
、![]() 、
、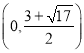 或
或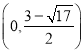
【解析】
(1)设抛物线的解析式为![]() ,代入点
,代入点![]() 的坐标即可求解;
的坐标即可求解;
(2)连接![]() ,可得点
,可得点![]() ,根据一次函数
,根据一次函数![]() 得出点
得出点![]() 、
、![]() 的坐标,然后利用三角形面积公式得出
的坐标,然后利用三角形面积公式得出![]() 的表达式,利用二次函数的表达式即可求解;
的表达式,利用二次函数的表达式即可求解;
(3)①当![]() 为直角边时,过点
为直角边时,过点![]() 和点
和点![]() 做垂线交
做垂线交![]() 轴于点
轴于点![]() 和点
和点![]() ,过点
,过点![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,得出
,得出![]() ,再利用等腰直角三角形和坐标即可求解;②当
,再利用等腰直角三角形和坐标即可求解;②当![]() 为斜边时,设
为斜边时,设![]() 的中点为
的中点为![]() ,以
,以![]() 为圆心
为圆心![]() 为直径做圆于
为直径做圆于![]() 轴于点
轴于点![]() 和点
和点![]() ,过点
,过点![]() 作
作![]() 轴,先得出
轴,先得出![]() 和
和![]() 的值,再求出
的值,再求出![]() 的值即可求解.
的值即可求解.
解:(1)一次函数![]() 与
与![]() 轴交于点
轴交于点![]() ,则
,则![]() 的坐标为
的坐标为![]() .
.
![]() 抛物线的顶点为
抛物线的顶点为![]() ,
,
![]() 设抛物线解析式为
设抛物线解析式为![]() .
.
![]() 抛物线经过点
抛物线经过点![]() ,
,
![]() .
.
![]() .
.
![]() 抛物线解析式为
抛物线解析式为![]() ;
;
(2)解法一:连接![]() .
.
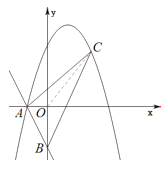
点![]() 为第一象限抛物线上一动点.点
为第一象限抛物线上一动点.点![]() 的横坐标为
的横坐标为![]() ,
,
![]() .
.
一次函数![]() 与
与![]() 轴交于点
轴交于点![]() .则
.则![]() ,
,
![]() 的坐标为
的坐标为![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
当![]() 时,
时,![]() 的值最大,最大值为
的值最大,最大值为![]() ;
;
解法二:作![]() 轴,交
轴,交![]() 于点
于点![]() .
.
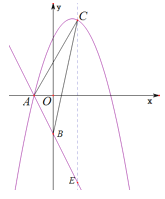
![]() 的坐标为
的坐标为![]() ,
,![]() .
.
点![]() 为第一象限抛物线上一动点.点
为第一象限抛物线上一动点.点![]() 的横坐标为
的横坐标为![]() ,
,
![]() ,
,![]() .
.
![]() .
.
![]() .
.
当![]() 时,
时,![]() 的值最大,最大值为
的值最大,最大值为![]() ;
;
解法三:作![]() 轴,交
轴,交![]() 于点
于点![]() .
.
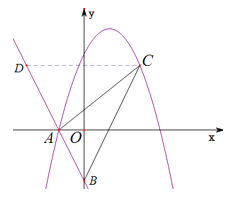
一次函数![]() 与
与![]() 轴交于点
轴交于点![]() .则
.则![]() ,
,
点![]() 为第一象限抛物线上一动点.点
为第一象限抛物线上一动点.点![]() 的横坐标为
的横坐标为![]() ,
,
![]() .
.
把![]() 代入
代入![]() ,解得
,解得![]() ,
,
![]() .
.
![]() .
.
当![]() 时,
时,![]() 的值最大,最大值为
的值最大,最大值为![]() ;
;
解法四:构造矩形![]() .(或构造梯形
.(或构造梯形![]() )
)
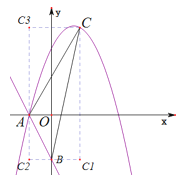
一次函数![]() 与
与![]() 轴交于点
轴交于点![]() .则
.则![]() ,
,
![]() 的坐标为
的坐标为![]() ,
,![]() .
.
点![]() 为第一象限抛物线上一动点.点
为第一象限抛物线上一动点.点![]() 的横坐标为
的横坐标为![]() ,
,
设点![]() 的纵坐标为
的纵坐标为![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
![]() .
.
当![]() 时,
时,![]() 的值最大,最大值为
的值最大,最大值为![]() ;
;
(3)由(2)易得点![]() 的坐标为
的坐标为![]() ,
,
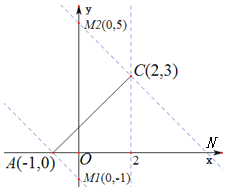
①当![]() 为直角边时,过点
为直角边时,过点![]() 和点
和点![]() 做垂线交
做垂线交![]() 轴于点
轴于点![]() 和点
和点![]() ,过点
,过点![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,如下图所示:
,如下图所示:
由点![]() 和点
和点![]() 的坐标可知:
的坐标可知:![]()
∴![]()
∴![]()
∴点![]() 的坐标为
的坐标为![]()
由题可知:![]()
∴![]()
∴点![]() 的坐标为
的坐标为![]() ;
;
②当![]() 为斜边时,设
为斜边时,设![]() 的中点为
的中点为![]() ,以
,以![]() 为圆心
为圆心![]() 为直径做圆于
为直径做圆于![]() 轴于点
轴于点![]() 和点
和点![]() ,过点
,过点![]() 作
作![]() 轴,如下图所示:
轴,如下图所示:
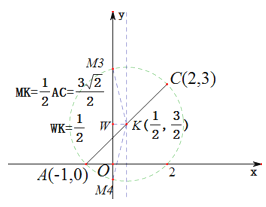
由点![]() 和点
和点![]() 的坐标可得点
的坐标可得点![]() 的坐标是
的坐标是![]()
∴![]() ,
,![]()
∴![]()
∴点![]() 的坐标为
的坐标为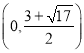 ,点
,点![]() 的坐标为
的坐标为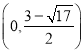
根据圆周角定理即可知道![]()
∴点![]() 和点
和点![]() 符合要求
符合要求
∴综上所述点![]() 的坐标为
的坐标为![]() 、
、![]() 、
、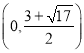 或
或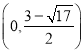 .
.


科目:初中数学 来源: 题型:
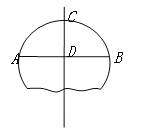
【题目】如图,破残的圆形轮片上,弦AB的垂直平分线交AB于C,交弦AB于D.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)若AB=24cm,CD=8cm,求(1)中所作圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别交x轴,y轴于A(4.0),B(0,2)两点,与反比例函数y=![]() 的图象交于C.D两点,CE⊥x轴于点E且CE=3.
的图象交于C.D两点,CE⊥x轴于点E且CE=3.
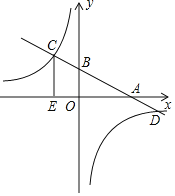
(1)求反比例函数与一次函数的解析式;
(2)根据图象直接写出:不等式0<kx+b<![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行,某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出50辆;若每辆自行车每降价20元,每月可多售出5辆,求该型号自行车降价多少元时,每月可获利30000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
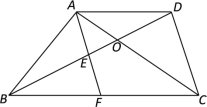
【题目】如图,在梯形ABCD中,AD//BC,AC与BD相交于点O,点E在线段OB上,AE的延长线与BC相交于点F,OD2 = OB·OE.
(1)求证:四边形AFCD是平行四边形;
(2)如果BC=BD,AE·AF=AD·BF,求证:△ABE∽△ACD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
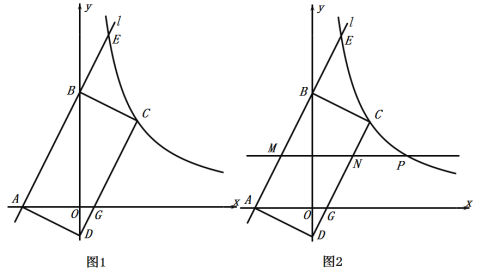
如图1,平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,
,![]() .双曲线
.双曲线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)求![]() 的值;
的值;
(2)在图1中以线段![]() 为边作矩形
为边作矩形![]() ,使顶点
,使顶点![]() 在第一象限、顶点
在第一象限、顶点![]() 在
在![]() 轴负半轴上.线段
轴负半轴上.线段![]() 交
交![]() 轴于点
轴于点![]() .直接写出点
.直接写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(3)如图2,在(2)题的条件下,已知点![]() 是双曲线
是双曲线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的平行线分别交线段
轴的平行线分别交线段![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
请从下列![]() ,
,![]() 两组题中任选一组题作答.我选择组题.
两组题中任选一组题作答.我选择组题.
A.①当四边形![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②在①的条件下,连接![]() ,
,![]() .坐标平面内是否存在点
.坐标平面内是否存在点![]() (不与点
(不与点![]() 重合),使以
重合),使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,直接写出点
全等?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
B.①当四边形![]() 成为菱形时,求点
成为菱形时,求点![]() 的坐标;
的坐标;
②在①的条件下,连接![]() ,
,![]() .坐标平面内是否存在点
.坐标平面内是否存在点![]() (不与点
(不与点![]() 重合),使以
重合),使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,直接写出点
全等?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了答谢顾客发起活动:凡在本超市一次性购物满100元的顾客,当天均可凭购物小票参与一次抽奖活动,奖品是三种瓶装饮品:红酒、啤酒和酸奶,抽奖规则如下:
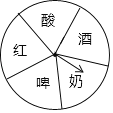
①如图,是一个材质均匀可自出转动的转盘,转盘被等分成五个扇形区域,各区域上分别写有“红”、“啤”、“酒”、“酸”、“奶”字样;
②参与一次奖活动的顾客可以进行两次“随机转动”,但若转盘停止时指针指向两边区域的边界则可以重新转动转盘,直到指针停到有字的区域才算完成了这次随机转动;
③顾客参与一次抽奖活动,记录两次指针所指区域对应的字,若这两个字和某种奖品名称对应的两个字相同(与字的顺序无关),便可获得相应奖品一瓶;若两字不能组成一种奖品名时,不能获得任何奖品,根据以上规则,回答下列问题:
(1)求只做一次“随机转动”指针指向“酒“字的概率;
(2)请用列表或画树状图的方法求顾客参与一次抽奖活动获得一瓶红酒的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+5ax+c(a<0)与x轴负半轴交于A、B两点(点A在点B的左侧),与y轴交于C点,D是抛物线的顶点,过D作DH⊥x轴于点H,延长DH交AC于点E,且S△ABD:S△ACB=9:16,
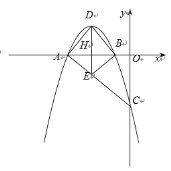
(1)求A、B两点的坐标;
(2)若△DBH与△BEH相似,试求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
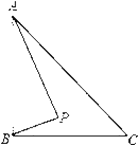
【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com