
分析 显然当小圆与扇形的两半径及弧相切时小圆最大,设小圆半径为r,继而根据OP+PF=1可得关于r的方程,解之可得r,再用扇形面积减去圆的面积即可得.
解答 解:如图,设⊙P的半径为r,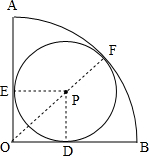
∴PD=PE=PF=r,
∵∠PEO=∠AOB=∠PDO=90°,
∴四边新PEOD为正方形,
∴PO=$\sqrt{2}$PE=$\sqrt{2}$r,
∴OF=OP+PF=$\sqrt{2}$r+r=1,
解得:r=$\sqrt{2}$-1,
则余下的图形的面积为$\frac{1}{4}$×π×12-π•($\sqrt{2}$-1)2=$\frac{8\sqrt{2}-11}{4}$π,
故答案为:$\frac{8\sqrt{2}-11}{4}$π.
点评 本题主要考查扇形面积的计算,根据题意求得内部最大圆的半径是解题的关键.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:选择题
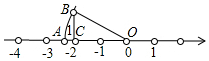 已知,如图,OA=OB,那么数轴上的点A所表示的数是( )
已知,如图,OA=OB,那么数轴上的点A所表示的数是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | -$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
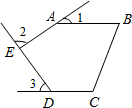 如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=( )
如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=( )| A. | 90° | B. | 180° | C. | 120° | D. | 270° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com